chapter: 4 カイ二乗検定（2 x 2）

【例題】サンプルデータ※データは架空　年齢によって，サンタクロースを信じるのかどうかが異なるかを調べるため，ある幼稚園の園児と，ある小学校の1年生にサンタクロースを信じるかどうか調査した。幼稚園児と小学生（1年生）でサンタクロースを信じる割合が異なるかを調べなさい。

　年齢は量的にもとらえることができるが，今回の場合は幼稚園児と小学生ということで，質的変数として扱う。サンタクロースを信じる・信じないというのは信念という質的変数となる。このように質的変数と質的変数との関連性を調べるときには，カイ二乗検定を用いる。

データの説明

変数名	内容	尺度水準
ID	ID	名義尺度
組	1 = Kindergartener（幼稚園児） 2 = Schoolchild（小学生）	名義尺度
信念	1 = Yes（信じる） 2 = No（信じない）	名義尺度

4.1 分析の実施

　値ラベルをデータの説明に従って設定

度数分布
伝統的の分割表

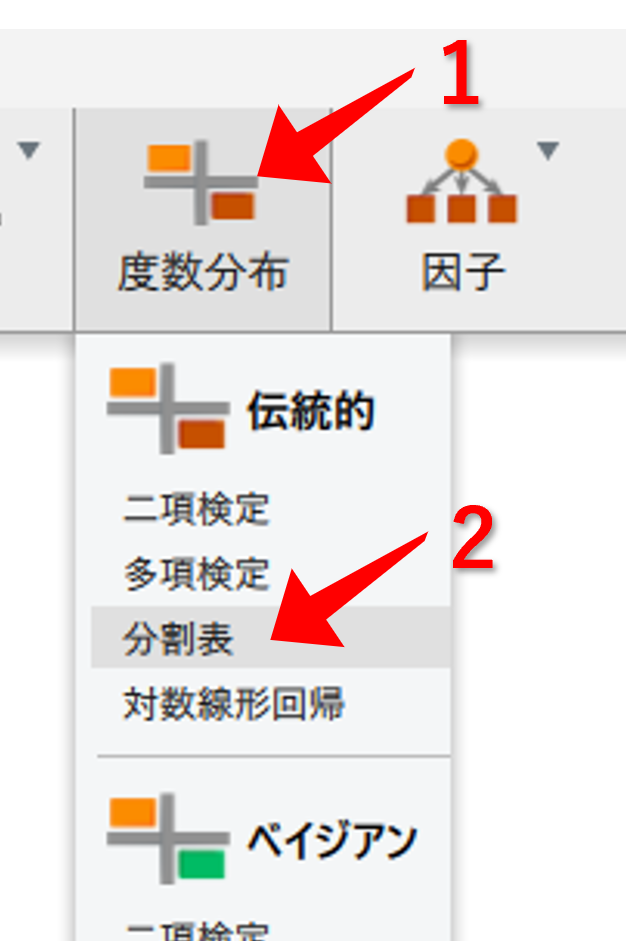
行に（原因的な）変数を移動
列に（結果的な）変数を移動
▶統計量を選択
\(χ^2\)を☑（デフォルトで入っている）
オッズ比（2x2のみ）を☑
▶セルを選択
カウントにある期待値を☑
パーセンテージにある行を☑

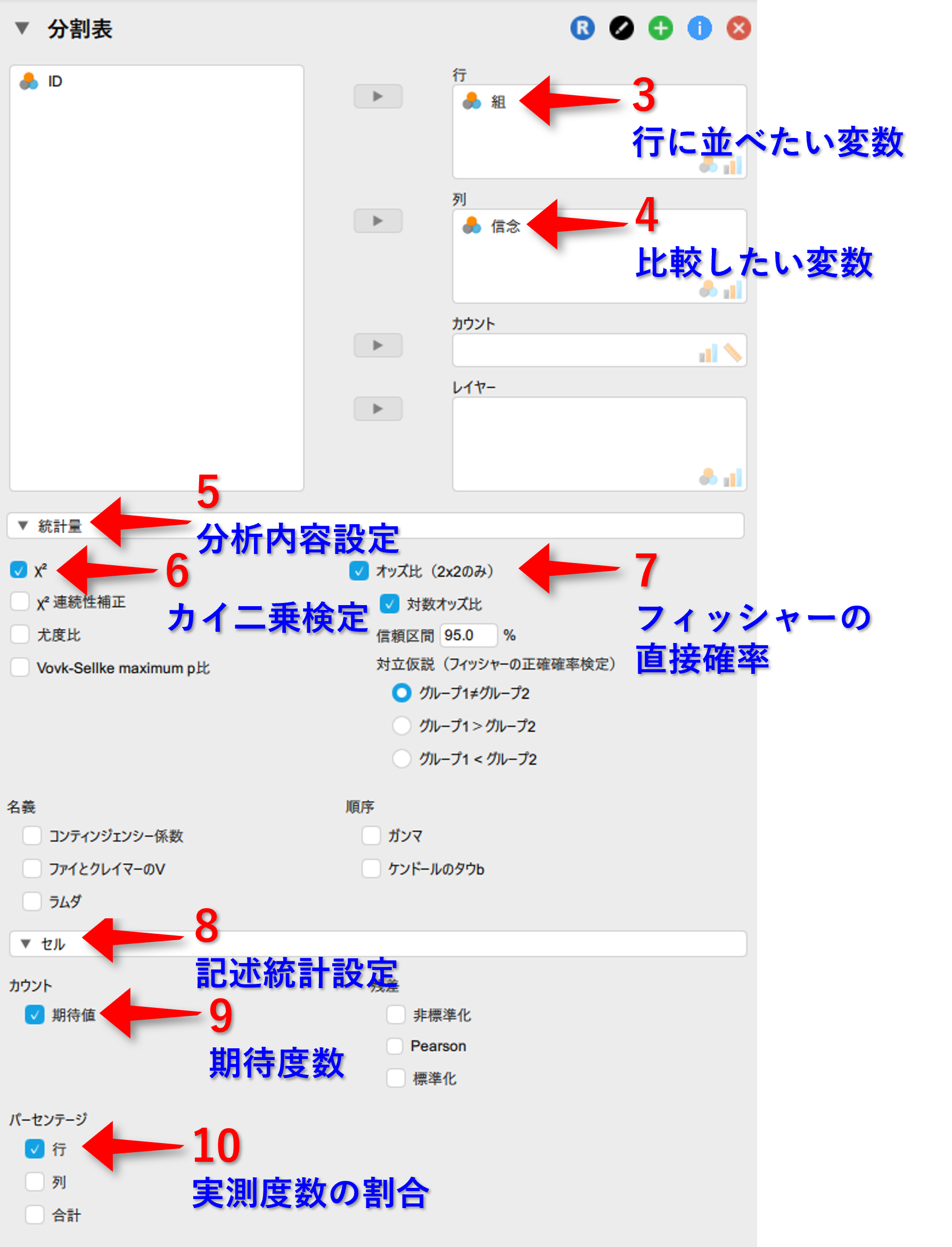
4.2 出力結果

分割表

　記述統計として，実測度数，割合をまとめたクロス集計表を作成する（赤色の部分）。

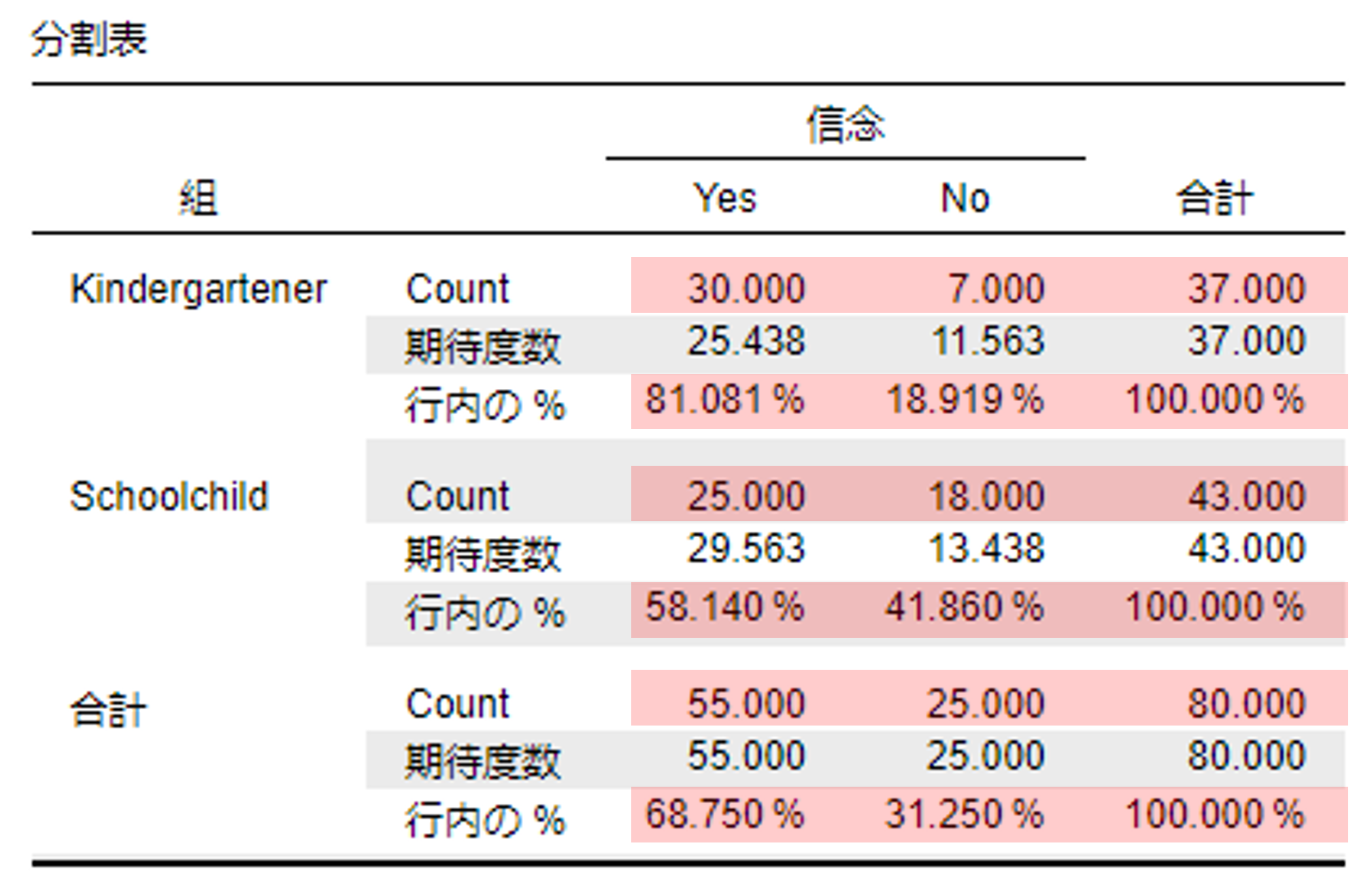
Countの行：実測度数
- 例えば，KindergartenerのうちYesと応えた人が30名
期待度数の行：期待度数
- 例えば，KindergartenerのうちYesと応えた人の期待度数は25.438（Kindergartener全体の人数×合計のYesの割合）
行内の%：行を100%としたときの割合
- 例えば，KindergartenerのうちYesと応えた人の割合が81.081%

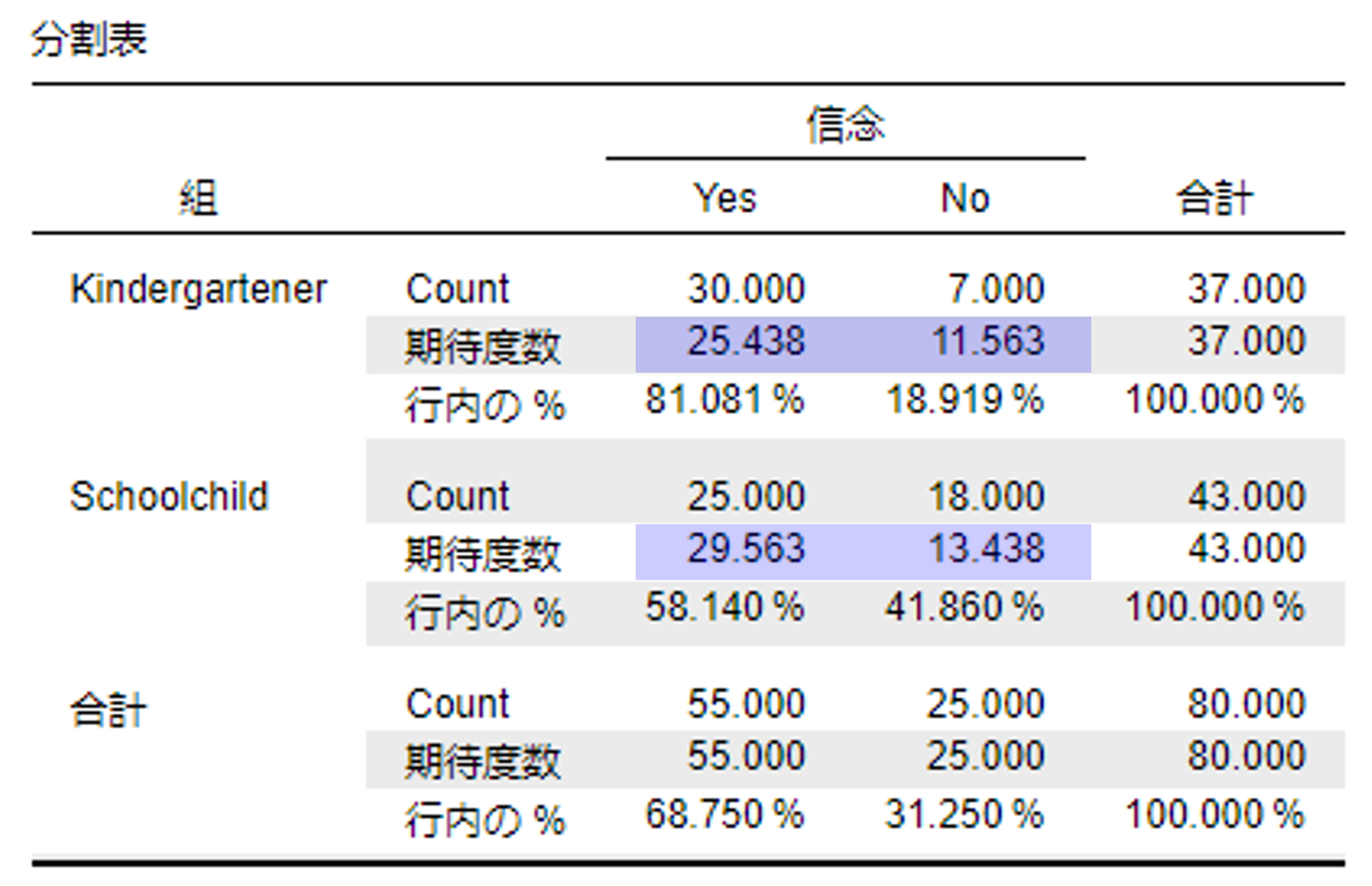
カイ二乗検定

　カイ二乗検定は，期待度数が5未満のセルが1セルでもある場合は用いることができない（青色の部分）。今回の場合，最小のセルでも11.563（幼稚園児の信じないと応えた人）であるため，カイ二乗検定を用いることができる。

　カイ二乗検定の結果は，\(χ^2\)の行に\(χ^2\)値（Value），自由度（df），有意確率（p）がまとめられている（赤色部分）。

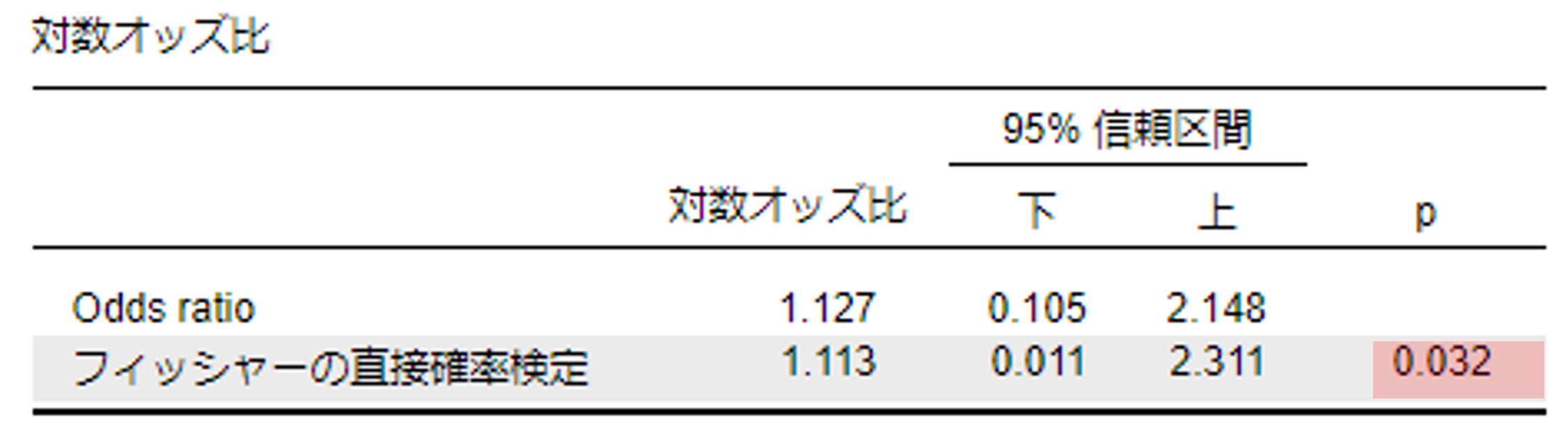
対数オッズ比

　一方，期待度数が5未満のセルが1セルでもある場合は，フィッシャーの直接確率を報告する。この期待度数にかかわらず，フィッシャーの直接確率を報告しても良い。

4.3 記述例

カイ二乗検定で記述する場合

　幼稚園の組によってサンタクロースを信じるかどうかに関係性があるかを検討するため，クロス集計を行った。サンタクロースを信じると応えた子どもは年少組では30名（81.8%），年長組では25名（58.1%）であった。そこで，カイ二乗検定を行ったところ，サンタクロースを信じる子どもの割合は，年長組よりも年少組の方が有意に多ことが明らかとなった（\(χ^2\) (1) = 4.87, p = .027）。

フィッシャーの直接確率で記述する場合