chapter: 5 カイ二乗検定(i x j)
【例題】サンプルデータ※データは架空 年齢によって,サンタクロースを信じるのかどうかが異なるかを調べるため,ある幼稚園の園児と,ある小学校の1年生にサンタクロースを信じるかどうか調査した。幼稚園児と小学生(1年生)でサンタクロースを信じる割合が異なるかを調べなさい。
年齢は量的にもとらえることができるが,今回の場合は幼稚園児と小学生ということで,質的変数として扱う。サンタクロースを信じる・信じない・わからないというのは信念という質的変数となる。このように質的変数と質的変数との関連性を調べるときには,カイ二乗検定を用いる。今回の例のように,組のときの水準数が2,信念のときの水準数が3のときは,2 x 3と呼び,このときにもカイ二乗検定を用いる。また,カイ二乗検定の結果が有意だったときには,どこに差があるかを調べるため,追加で,残差分析を行う。
データの説明
| 変数名 | 内容 | 尺度水準 |
|---|---|---|
| ID | ID | 名義尺度 |
| Generation | 1 = Kindergartener(幼稚園児) 2 = Schoolchild(小学生) |
名義尺度 |
| Belief | 1 = Yes(信じる) 2 = No(信じない) 3 = Not Sure(わからない) |
名義尺度 |
5.1 分析の実施
値ラベルをデータの説明に従って設定
1~6は通常の2x2のときと同様
度数分布伝統的の
分割表行に(原因的な)変数を移動
列に(結果的な)変数を移動
▶統計量を選択\(χ^2\)を☑(デフォルトで入っている)
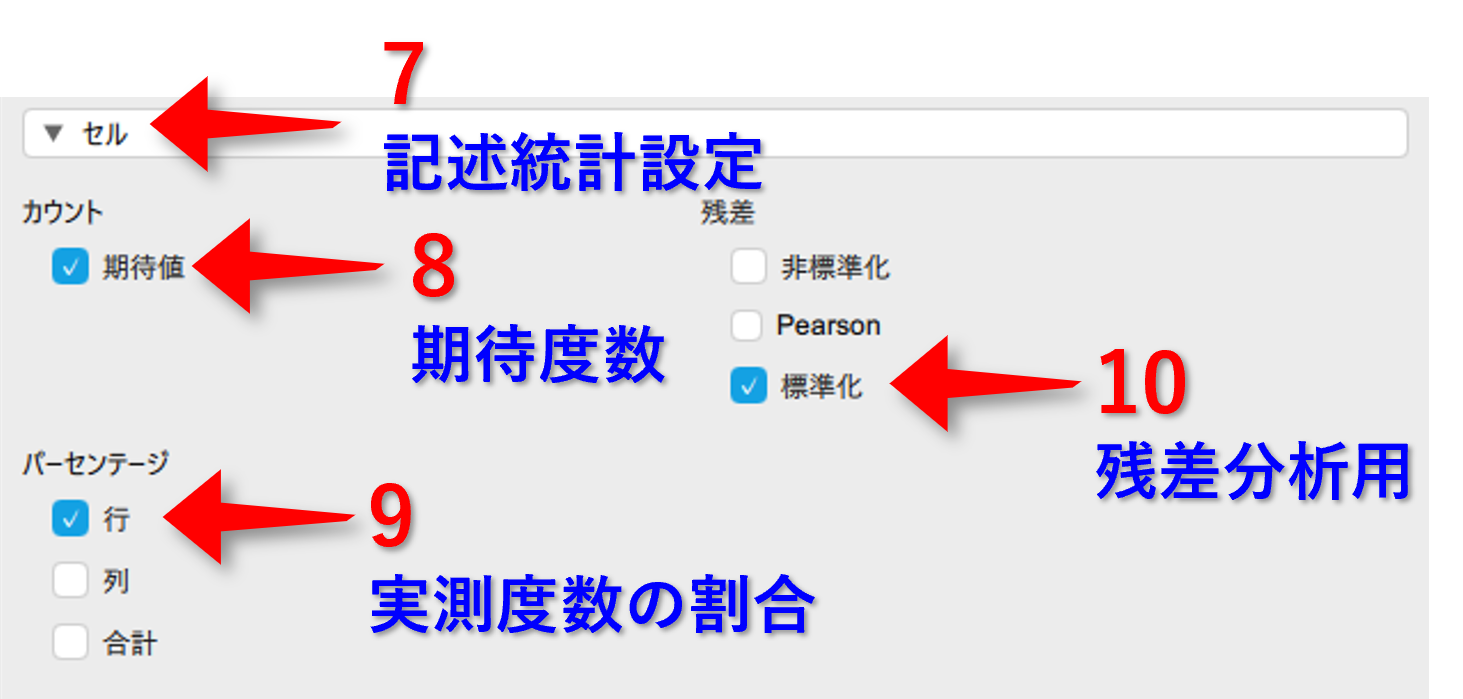
▶セルを選択カウントにある期待値を☑
パーセンテージにある行を☑
残差にある標準化を☑
5.2 出力結果
出力結果の見方もこれまでと同様
分割表
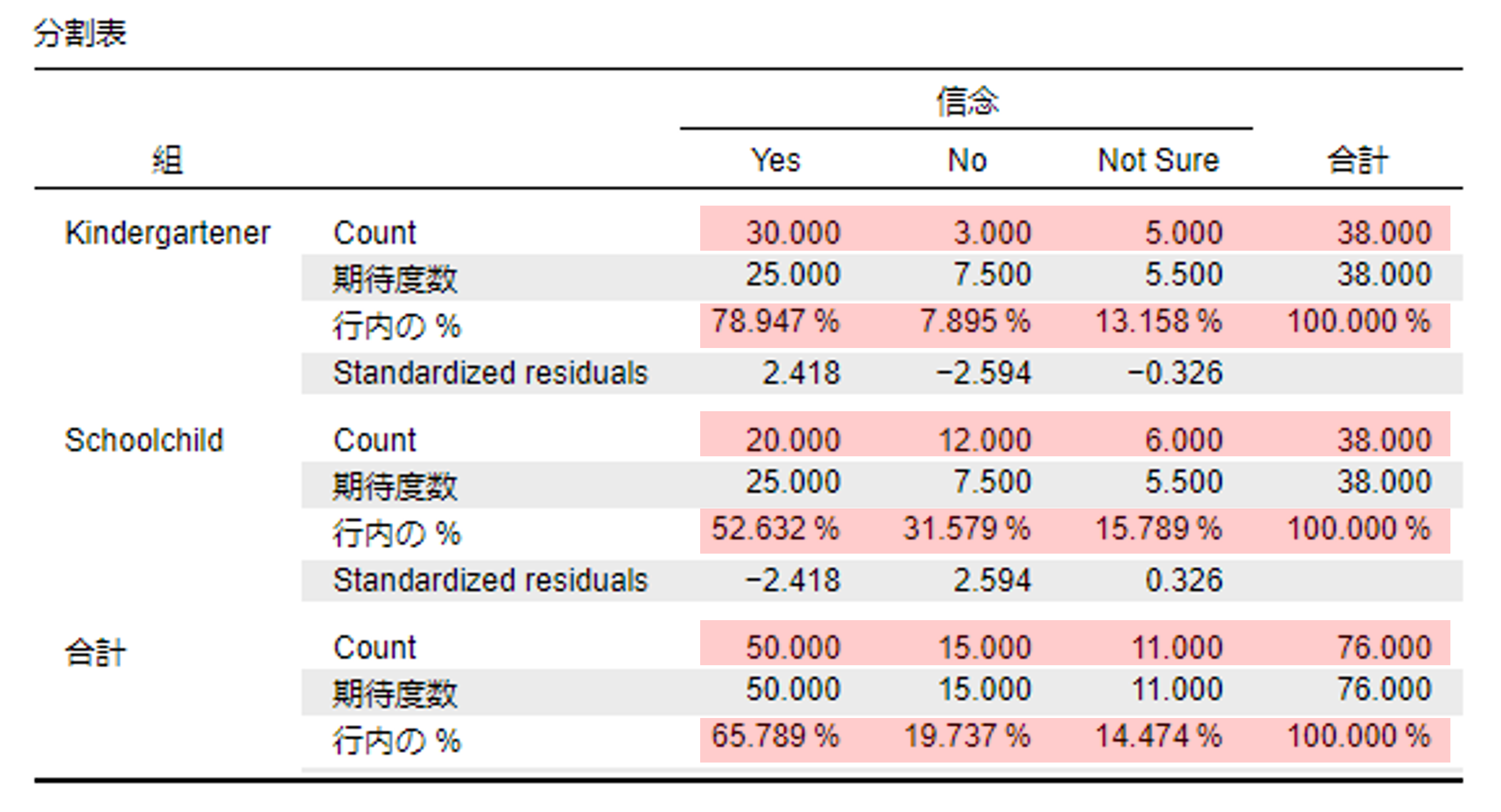
記述統計として,実測度数,割合をまとめたクロス集計表を作成する(赤色の部分)。
- Countの行:実測度数
- 例えば,KindergartenerのうちYesと応えた人が30名
- 期待度数の行:期待度数
- 例えば,KindergartenerのうちYesと応えた人の期待度数は25.000(Kindergartener全体の人数×合計のYesの割合)
- 行内の%:行を100%としたときの割合
- 例えば,KindergartenerのうちYesと応えた人の割合が78.947%
- Standardized residuals:調整済み残差(残差分析に必要)
- 例えば,KindergartenerのうちYesと応えた人の割合が78.947%
カイ二乗検定
カイ二乗検定の結果は,\(χ^2\)の行に\(χ^2\)値(Value),自由度(df),有意確率(p)がまとめられている(赤色の部分)。

カイ二乗検定の結果は,\(χ^2\) (2) = 7.49, p = .024であり,有意であった。しかし,この結果は,具体的にどこに差があるかはわからないため,引き続き残差分析を行う。
5.3 残差分析
カイ二乗検定(i x j)の結果,有意だった際には,引き続き残差分析を行う必要がある。しかし,JASPでは残差分析の結果は算出されない。しかし,ver.0.17.1より残差が算出されるようになったため,そこから有意確率を算出した上で,最終的な判断をする。 調整済み残差は正規分布に従って,有意性検定を行うため,以下のように値が決まっている。
| 残差の絶対値 | 有意確率 |
|---|---|
| ≧1.65 | p < .10 |
| ≧1.96 | p < .05 |
| ≧2.58 | p < .01 |
つまり,α = .05(有意水準を5%)としたときには,残差の絶対値が1.96以上になるときに,有意確率が5%未満になる。
また,具体的な数値を知りたいときや表を作成するときには,以下のエクセルを使うことによって,簡単に算出することができる(2x3から2x5に対応)。
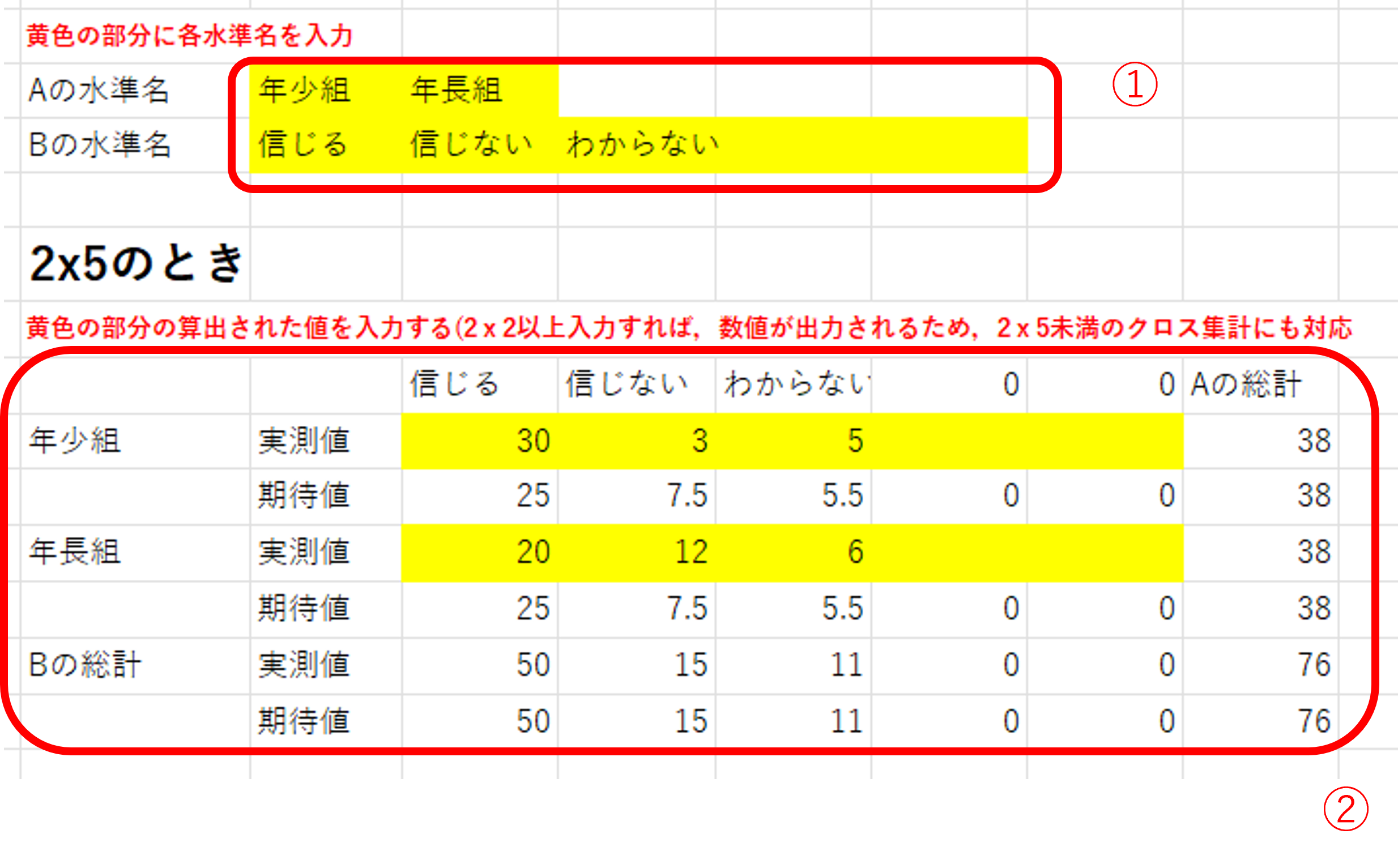
- 水準名の黄色部分に水準名を入力
- 表の部分に分割表に得られた実測度数を入力
- 2の右側に調整済み残差と有意確率が自動的に反映されるため,そこから残差分析の結果を判断
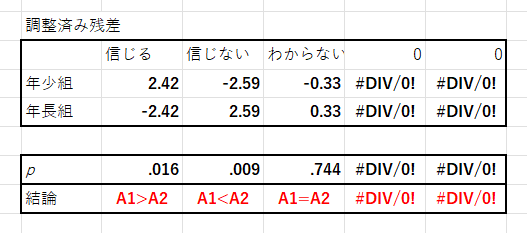
※判定の結果も等号・不等号で表される
5.4 記述例
幼稚園の組によってサンタクロースを信じるかどうかに関係性があるかを検討するため,クロス集計を行った。サンタクロースを信じると応えた子どもは年少組では30名(78.9%),年長組では20名(52.6%),信じないと応えた子どもは年少組では3名(7.9%),年長組で12名(31.6%),わからないと応えた子どもは年少組では5名(13.2%),年長組では6名(15.8%)であった。そこで,カイ二乗検定を行ったところ,サンタクロースに対する信念が組によって有意に異なった(\(χ^2\) (2) = 7.49, p = .024)。そこで,残差分析を行ったところ,表1のようになり,サンタクロースを信じる子どもは,年長組よりも年少組の方が有意に多く,サンタクロースを信じない子どもは,年少組よりも年長組の方が有意に多くなった。一方,わからないと応えた子どもに組による有意な差はないことが明らかとなった。
