chapter: 6 t検定(対応のない)
【例題】サンプルデータ※データは架空 中学1年生と中学3年生とで,授業内の質問数が異なるかを調べるため,ある中学校の中学1年生と中学3年生のクラスの1ヶ月間の授業内の質問数を測定した。学年によって授業内の質問数が異なるかを調べなさい。
中学1年生と中学3年生は学年という質的変数,授業内の質問数は質問数という量的変数となる。質的変数においては,2水準(中学1年生と中学3年生)であり,これらは異なる人の比較となる。このように異なる質的変数(2水準)と量的変数との関連性を調べるときには,対応のないt検定(Welchのt検定)を用いる。
データの説明
| 変数名 | 内容 | 尺度水準 |
|---|---|---|
| ID | ID | 名義尺度 |
| SchoolYear | 1 = 1st(中学1年生) 2 = 3rd(中学3年生) |
名義尺度 |
| Question | 1ヶ月間の授業内の質問数 | 比率尺度(スケール) |
6.1 分析の実施
値ラベルをデータの説明に従って設定
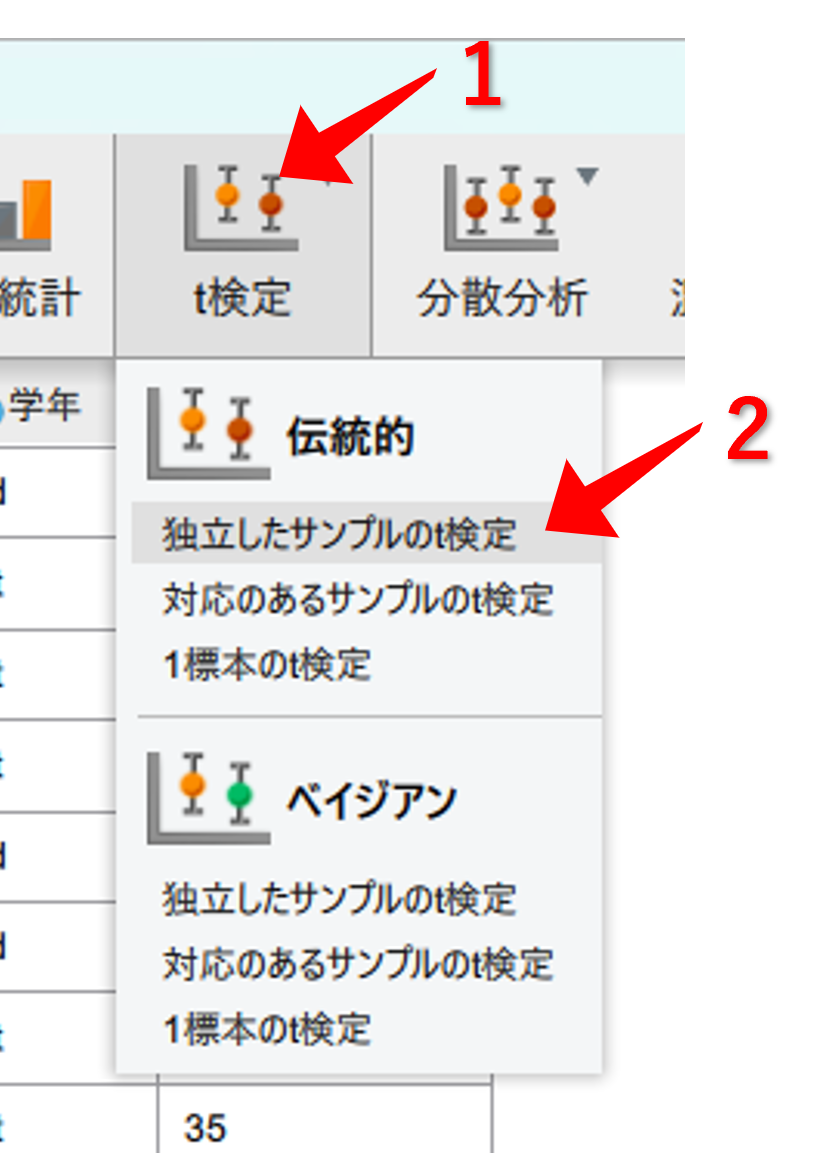
t検定- 伝統的の
独立したサンプルのt検定
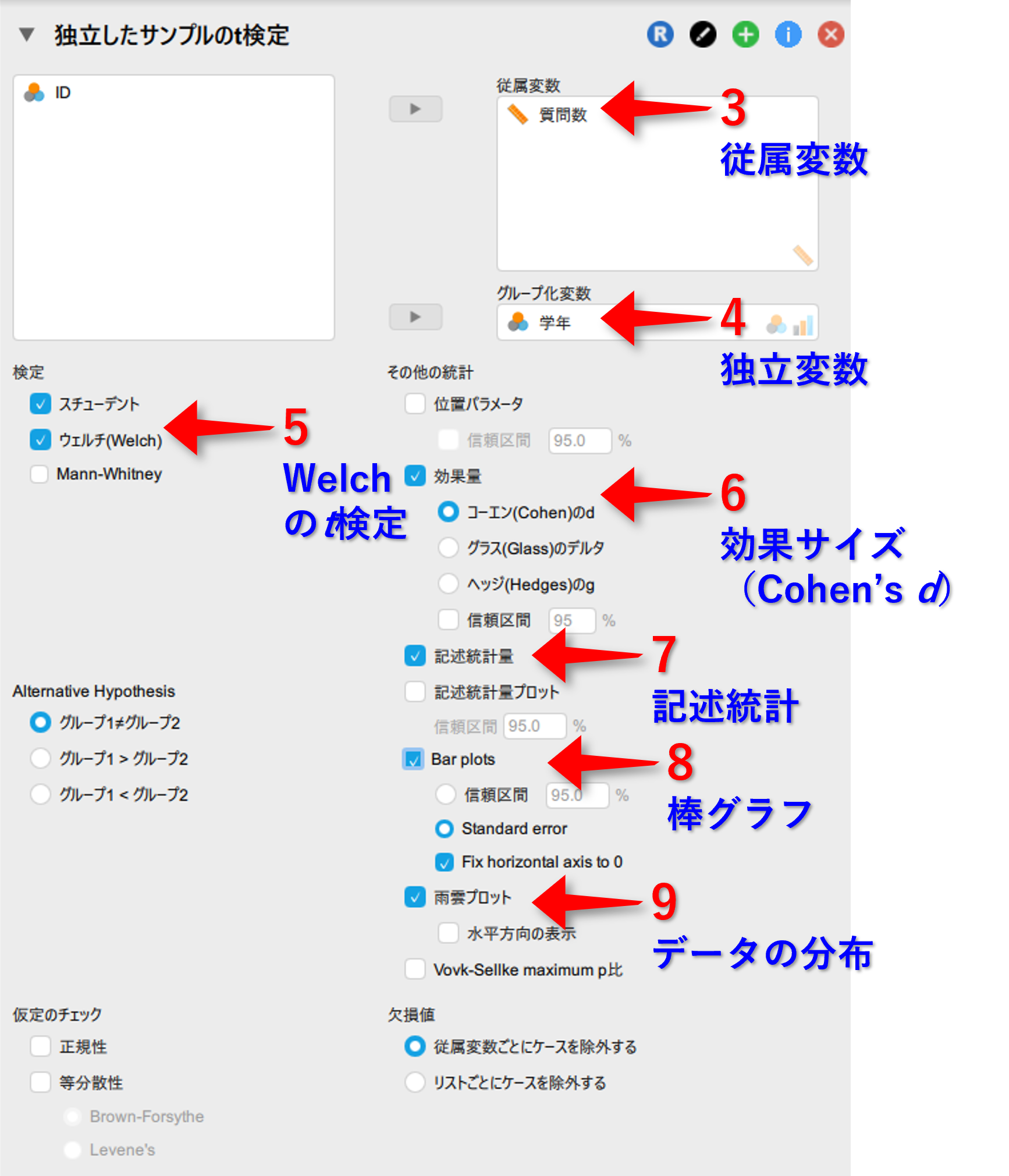
- 従属変数に(量的)変数を移動
- グループ化変数に(質的)変数を移動
- 検定の中にあるウェルチ(Welch)を☑(スチューデントは☑のままでも外しても良い)
- その他の統計にある効果量を☑にし,コーエン(Cohen)のdを選ぶ
- その他の統計にある記述統計量を☑
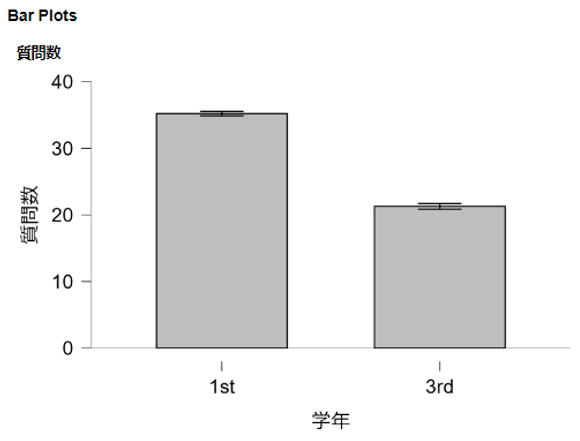
- その他の統計にあるBar plotsを☑
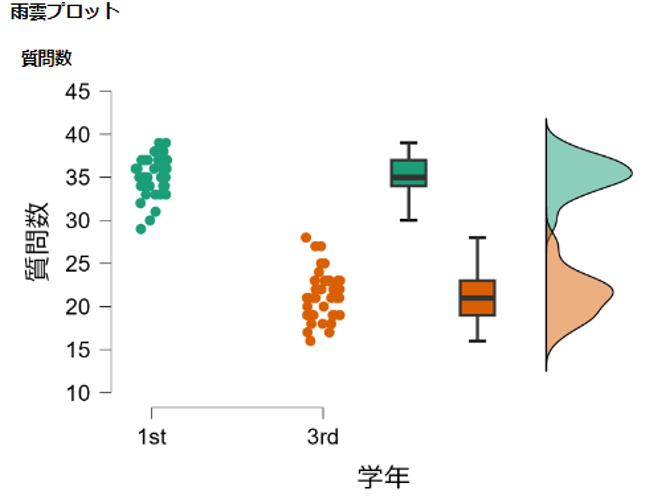
- その他の統計にある雨雲プロットを☑ (その他の統計にある記述統計量プロットでも良い)