chapter: 12 2要因分散分析（被験者内計画）

【例題】サンプルデータ※データは架空 　お店によって，ホットコーヒーとアイスコーヒーのどちらがおいしいかを調べるため，A社とB社のコーヒー（ホット・アイス）すべてを20名の人に飲んでもらい，おいしさの評定を行った（20点満点）。お店によって得意なコーヒーがあるのかを検討しなさい。

　A社とB社はお店という質的変数，ホットコーヒーあるいはアイスコーヒーは温度という質的変数，おいしさは量的変数となる。このように，質的変数が大きく2種類あることは2要因となり，それぞれ同じ人のデータを比較する場合，2要因分散分析（被験者内計画）を用いる。

データの説明

変数名 内容 尺度水準
ID ID 名義尺度
A_Hot A社のホットコーヒーのおいしさ 比率尺度（スケール）
A_Ice A社のアイスコーヒーのおいしさ 比率尺度（スケール）
B_Hot B社のホットコーヒーのおいしさ 比率尺度（スケール）
B_Ice B社のアイスコーヒーのおいしさ 比率尺度（スケール）

12.1 分析の実施（分散分析）

  1. 分散分析
  2. 伝統的の反復測定分散分析

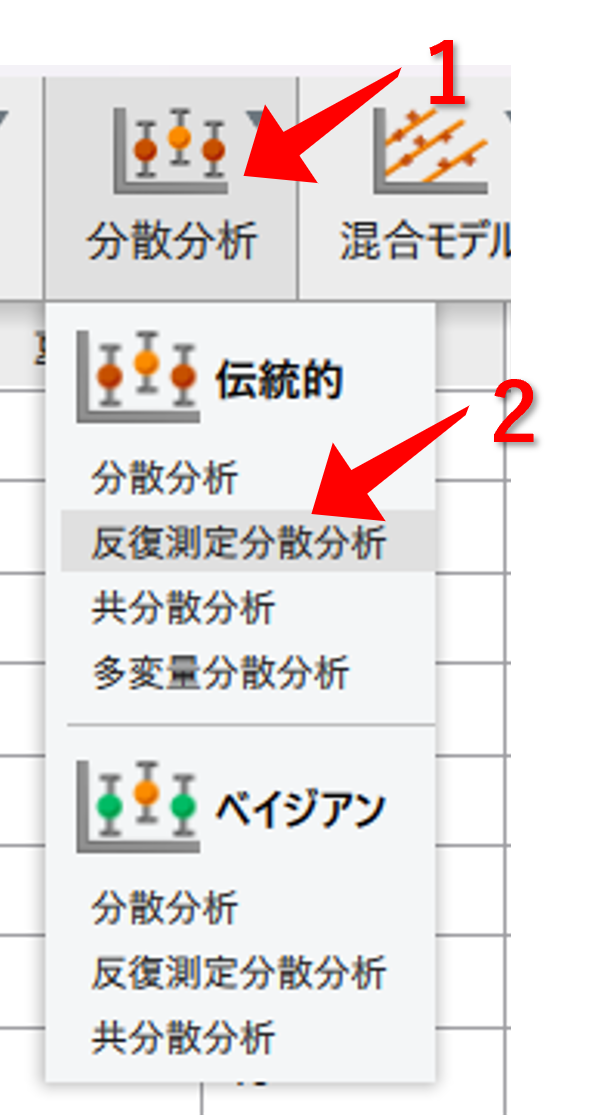
  1. 一つ目の要因名を入力
  2. 3で入力した要因の水準名を入力
  3. 二つ目の要因名を入力
  4. 5で入力した要因の水準名を入力
  5. 4と6で入力した名前に対応するデータを移動する
  6. 表示の中の記述統計を☑にする
  7. 表示の中の効果量の推定値を☑にし，η2<>と偏ηp2と一般化ηp2を☑

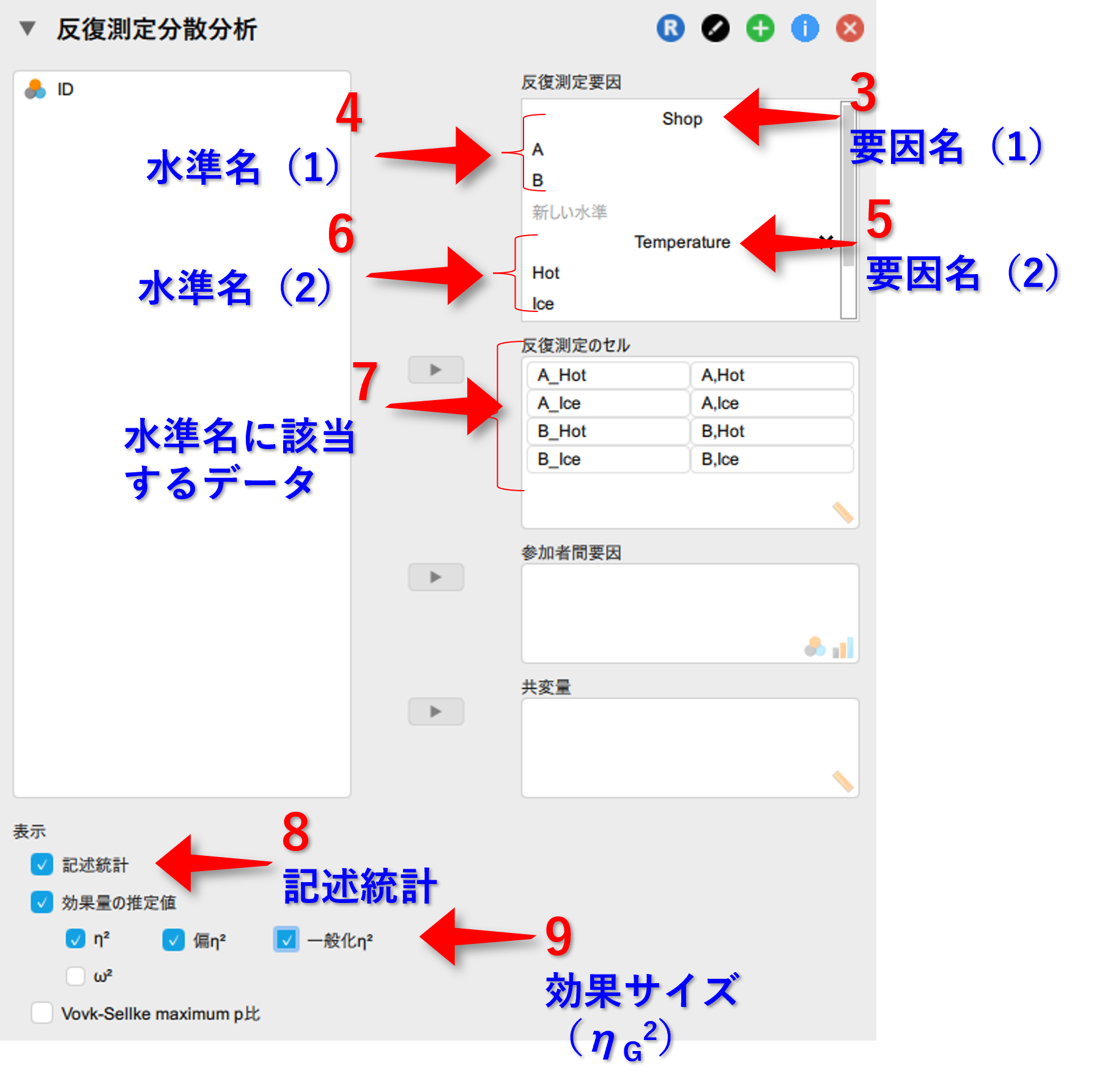
  1. ▶記述統計量プロットをクリック
  2. 横軸に独立変数の１つ移動
  3. 分割線に独立変数のもう１つを移動
  4. 表示の中にあるエラーバーの表示を☑
  5. Y軸のラベルに従属変数名を入力
  6. ▶雨雲プロットをクリック
  7. 横軸に独立変数の１つ移動
  8. 分割線に独立変数のもう１つを移動
  9. Y軸のラベルに従属変数名を入力

  1. ▶周辺平均をクリック
  2. それぞれの独立変数を移動

12.2 出力結果（分散分析）

記述統計量

　記述統計として，平均値，標準偏差を図か表でまとめる。

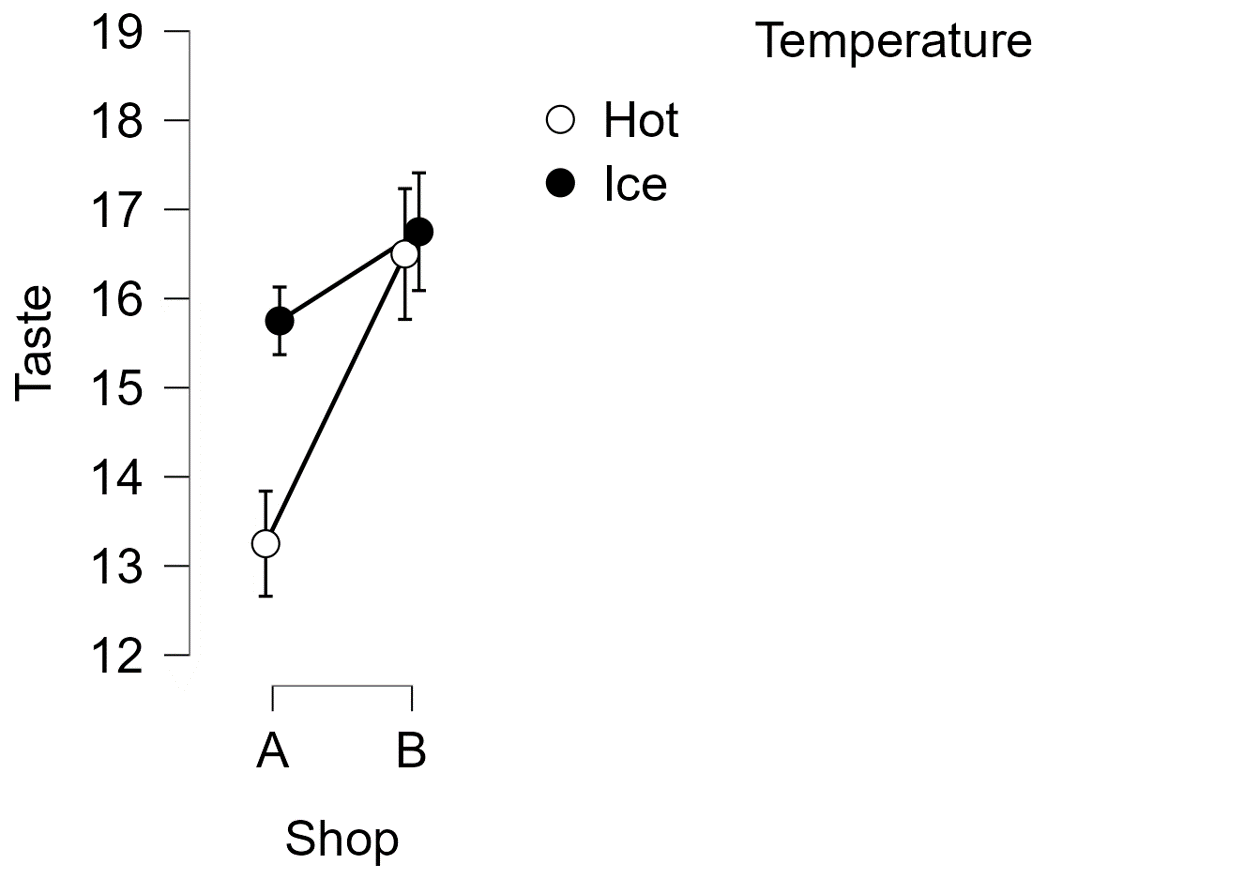
　データがどのように分布しているかを確認するために，雨雲プロットも確認する。

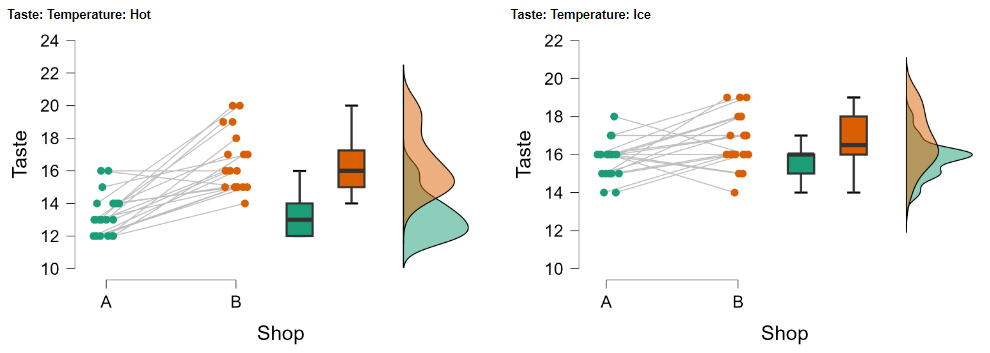
　さらに，片方の要因をつぶした平均値も算出されている。これは主効果の大小関係を把握する際に用いることができる。

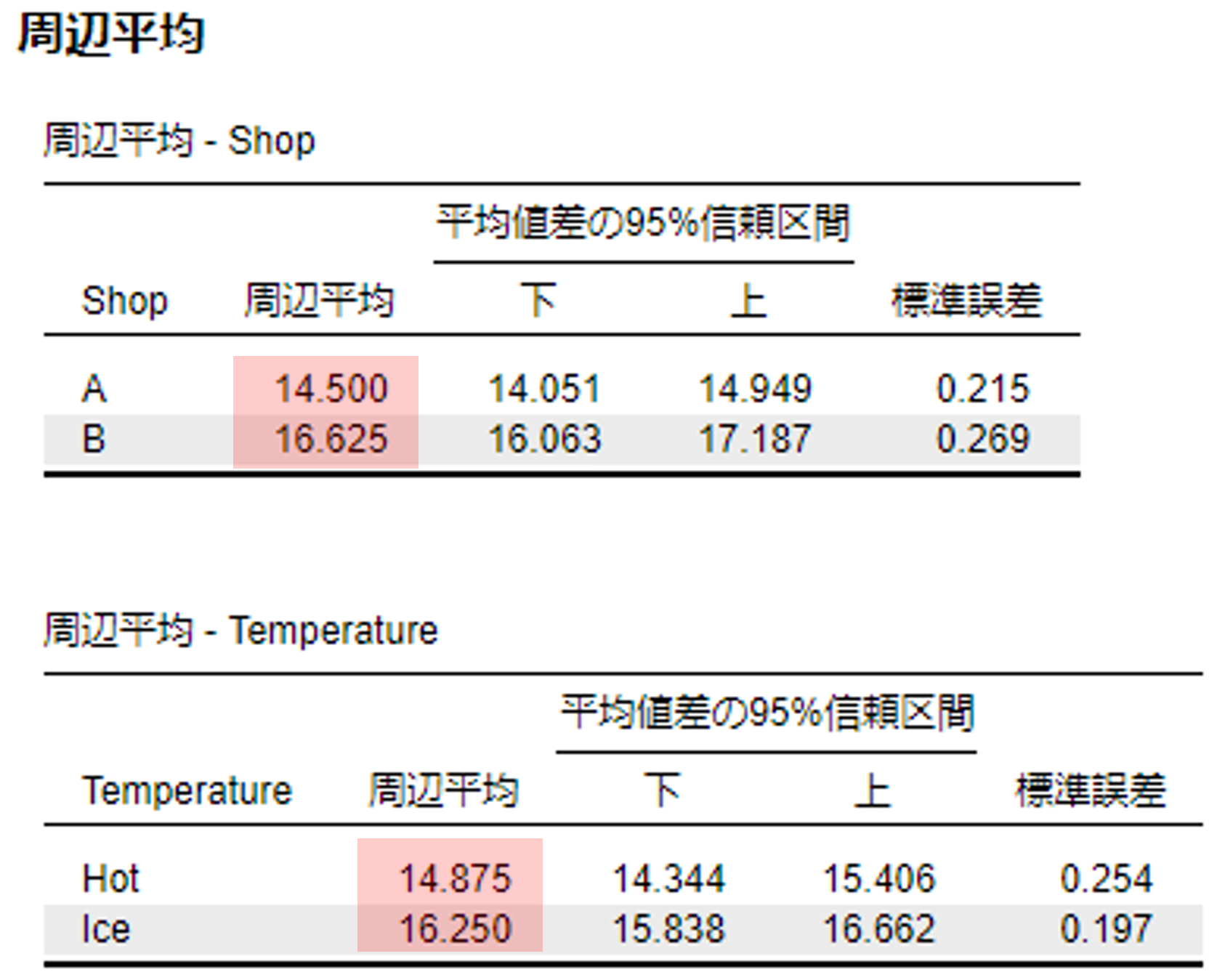
ANOVA

　分散分析の結果は，F値（F），自由度２つ（df），有意確率（p），効果サイズ（η2，ηp2，ηG2）がまとめられている。また，2要因以上の分散分析の場合，要因の数だけ主効果，要因同士の組み合わせの数だけ交互作用が算出される。具体的な出力結果は，Caseの中の単独の要因名，交互作用の結果はCaseの中の「要因名＊要因名」となっている。 　今回の場合，お店の行は教材の主効果，温度の行は授業形式の主効果，お店*温度の行はお店×温度の交互作用の結果となる。

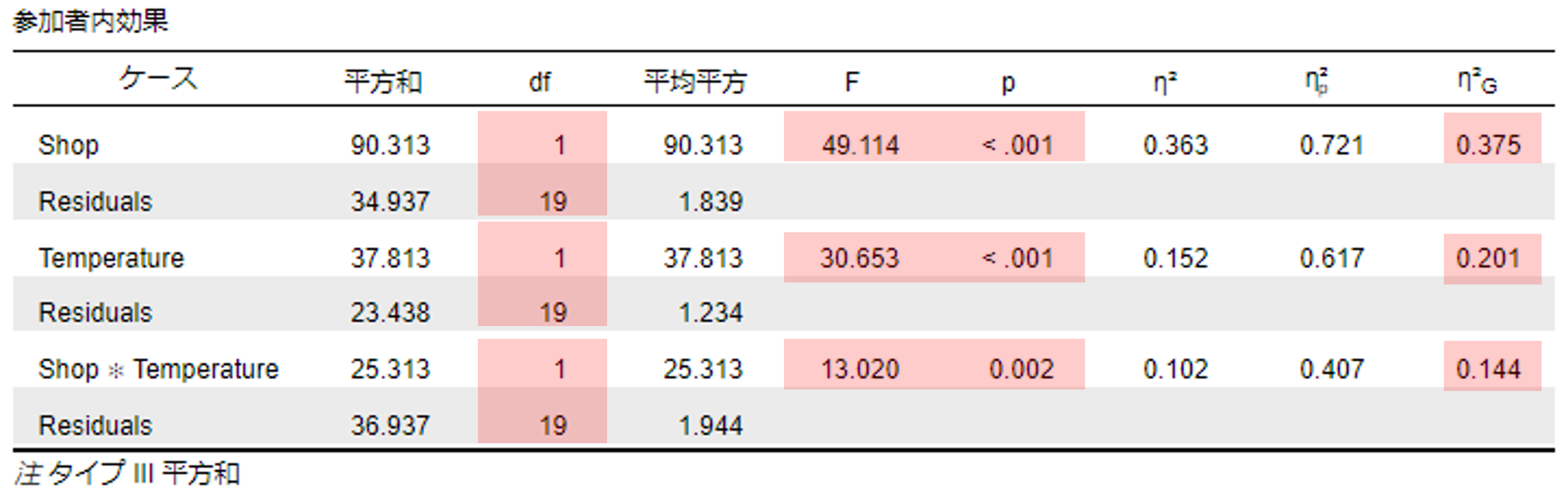
　上述の結果をまとめると以下の通りである。

  • お店の主効果（1,2行目）：F(1, 19) = 49.114, p < .001, ηG2 = .375
    • お店間に差があり，平均値から判断して，B社（M = 16.63）の方がA社（M = 14.50）よりも有意においしさの得点が高い
  • 温度の主効果（3,4行目）：F(1, 19) = 30.653, p < .001, ηG2 = .201
    • 温度間に差があり，平均値から判断して，アイスコーヒー（M = 16.25）の方がホットコーヒー（M = 14.88）よりも有意においしさの得点高い
  • お店×温度の交互作用（5,6行目）：F(1, 19) = 13.020, p = .002, ηG2 = .144
    • この結果は，具体的にどのような組み合わせに差があるかはわからないため，その組み合わせを明らかにするため，単純主効果の検定を行う必要がある

12.3 単純主効果の検定

  1. ▶単純主効果をクリック
  2. 単純効果を検討する要因に差があるかどうかを調べたい変数を１つ移動する
  3. 調整要因1にもう1つの変数を１つ移動する

12.4 出力結果

お店要因についての単純主効果（Simple Main Effects - Material）

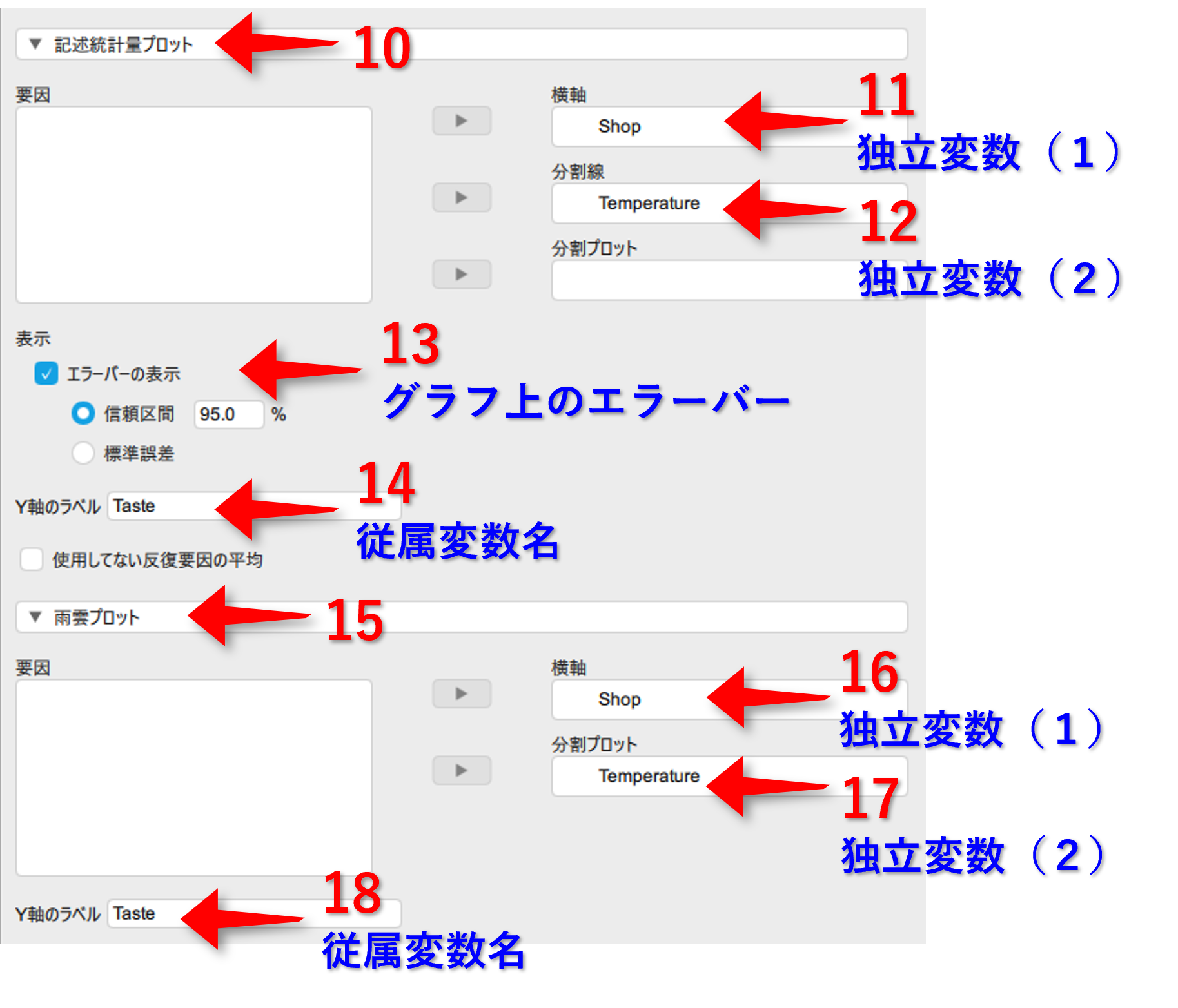
　調整要因（⑰）毎に検討する要因（⑯）があるかの結果が出力されている。これらの結果に報告に必要なものは，F値（F），自由度２つ（df），有意確率（p）となる。自由度の2つ目は，分散分析の結果におけるResidualsとなる。

　上述の結果をまとめると以下の通りである。

  • ホットコーヒーにおけるお店の単純主効果（1行目）：F(1, 19) = 43.747, p < .001
    • ホットコーヒーにおいて，A社はB社よりも有意に得点が低いことを表す（平均値から判断）
  • アイスコーヒーにおけるお店の単純主効果（2行目）：F(1, 19) = 7.308, p = .014
    • アイスコーヒーにおいて，A社はB社よりも有意に得点が低いことを表す（平均値から判断）

温度要因についての単純主効果（Simple Main Effects - Lecture）

　単純主効果の検定は，もう一方の要因についても調べることができる。具体的な方法は，14と15の手順で扱う要因をそれぞれ入れ替えることによって，算出される。入れ替えた後の結果は，以下の通りとなる。

　上述の結果をまとめると以下の通りである。

  • A社における温度の単純主効果（1行目）：F(1, 19) = 81.897, p < .001
    • A社において，アイスコーヒーの方がアイスコーヒーよりも有意においしさの得点が高いことを表す（平均値から判断）
  • B社における温度の単純主効果（2行目）：F(1, 19) = 0.259, p = .617
    • B社において，ホットコーヒーとアイスコーヒーにおいしさの得点の有意な差はない

12.5 記述例

※通常は記述統計は表やグラフにまとめる

　お店によって得意なコーヒーがあるのかを検討しなさい。おいしさ得点を従属変数とするお店×温度の2要因被験者内計画の分散分析を行った。その結果，お店の主効果が有意となり（F(1, 19) = 49.115, p < .001, ηG2 = .375），B社（16.63点）の方がA社（14.50点）よりもおいしさ得点が高いことが明らかとなった。また，温度も主効果が有意となり（F(1, 19) = 30.653, p < .001, ηG2 = .201），アイスコーヒー（16.25点）の方がホットコーヒー（14.88点）よりもおいしさ得点が高いことが明らかとなった。
　さらに，お店×おいしさの交互作用が有意となった（F(1, 19) = 13.020, p = .002, ηG2 = .144）。そこで，単純主効果の検定を行ったところ，A社においては，アイスコーヒー（M = 15.75, SD = 0.97）の方がホットコーヒー（M = 13.25, SD = 1.29）よりも有意においしさ得点が高いことが明らかとなった（F(1, 19) = 81.897, p < .001）。一方，B社においては，ホットコーヒー（M = 16.50, SD = 1.82）とアイスコーヒー（M = 16.75, SD = 1.41）の間に有意な差は見られなかった（F(1, 19) = 0.259, p = .617）。