chapter: 9 一元配置分散分析(被験者内計画)
【例題】サンプルデータ※データは架空 季節によって,学習意欲が異なるのかを調べるため,高校3年生に対して,春(4月),夏(7月),秋(10月),冬(1月)に毎回同じ人に質問紙による学習意欲調査(20点満点)を行った。季節によって学習意欲が異なるかを調べなさい。
春,夏,秋,冬は季節という質的変数,学習意欲は量的変数となる。質的変数においては,4水準(各季節)であり,これらは同じ人の比較となる。このように異なる質的変数(3水準以上)と量的変数との関連性を調べるときには,一元配置分散分析(被験者内計画)を用いる。
データの説明
| 変数名 | 内容 | 尺度水準 |
|---|---|---|
| ID | ID | 名義尺度 |
| Apr | 春(4月)の学習意欲得点 | 比率尺度(スケール) |
| Jul | 夏(7月)の学習意欲得点 | 比率尺度(スケール) |
| Oct | 秋(10月)の学習意欲得点 | 比率尺度(スケール) |
| Jan | 冬(1月)の学習意欲得点 | 比率尺度(スケール) |
9.1 分析の実施
分散分析- 伝統的の
反復測定分散分析
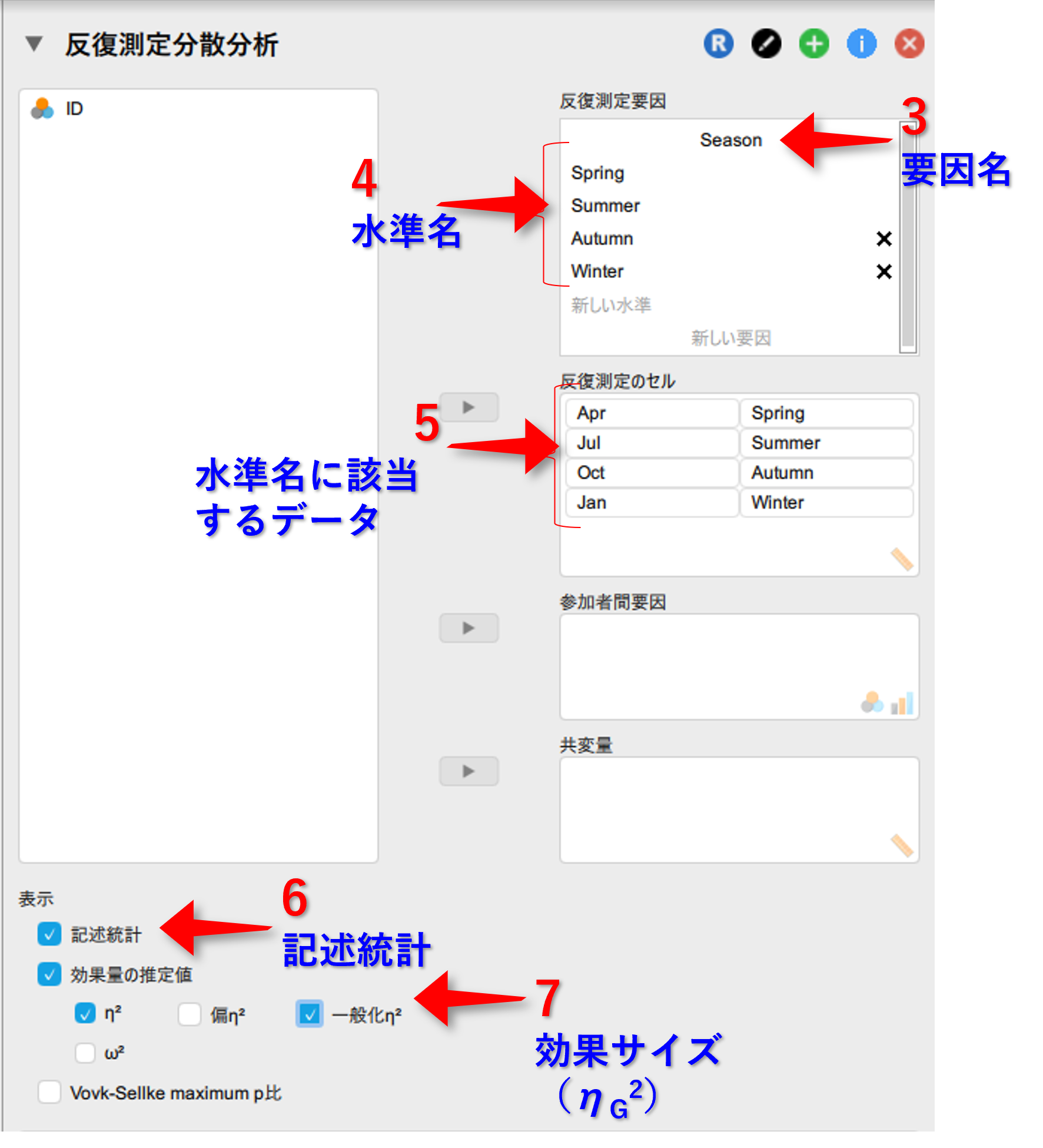
- 反復測定要因の中の新しい要因に分析する要因名を入力
- 水準に水準名を入力
- 3,4で入力したものが反復測定のセルに反映されるので,それぞれに対応したデータを移動する
- 表示の中の記述統計を☑
- 表示の中の効果量の推定値を☑にし,η2<>とηp2を☑
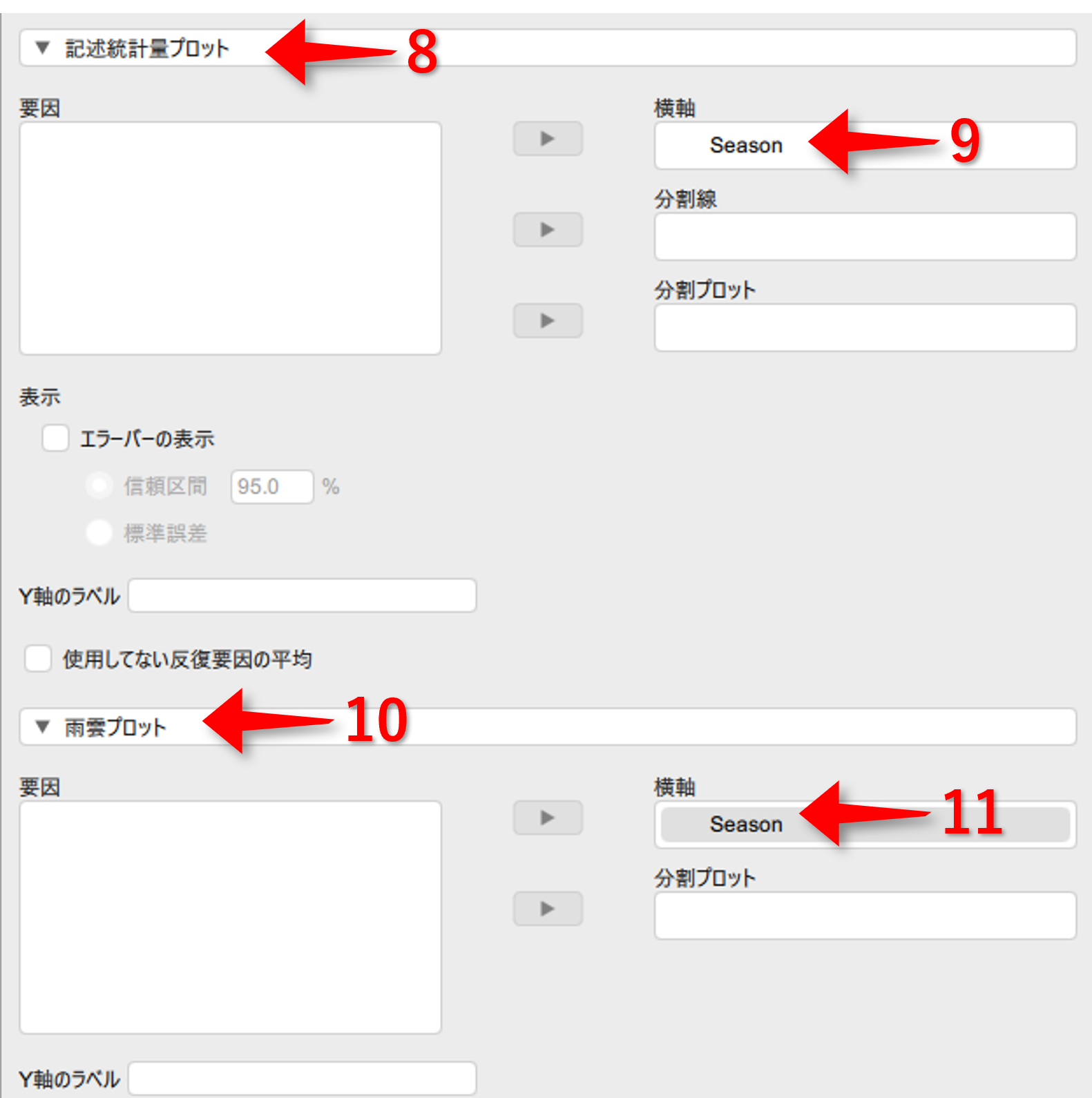
▶記述統計量プロットをクリック- 横軸に(質的)変数を移動する
▶雨雲プロットをクリック- 横軸に(質的)変数を移動する
9.2 出力結果(1)
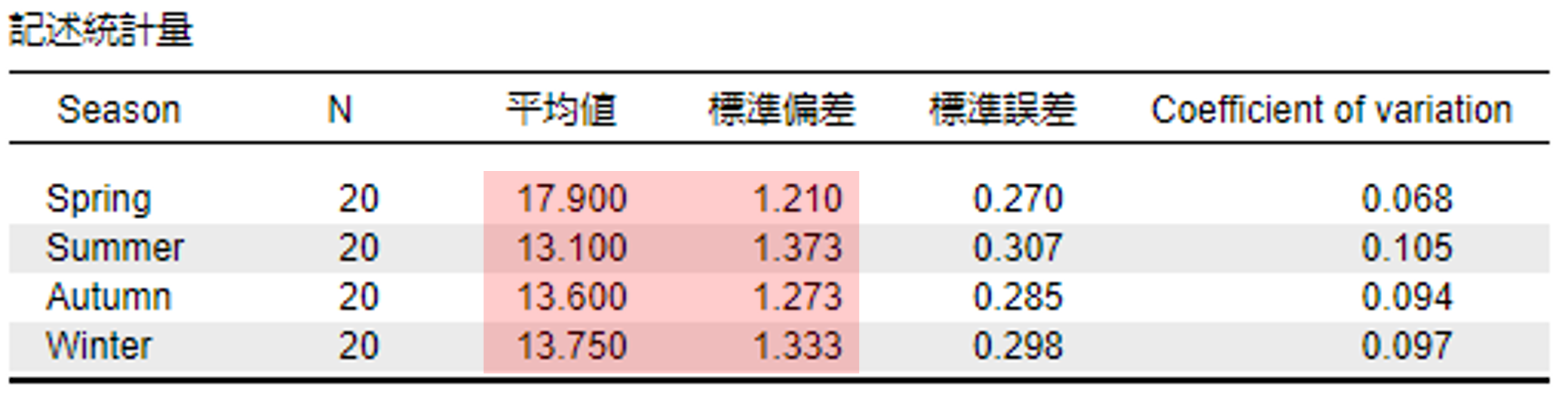
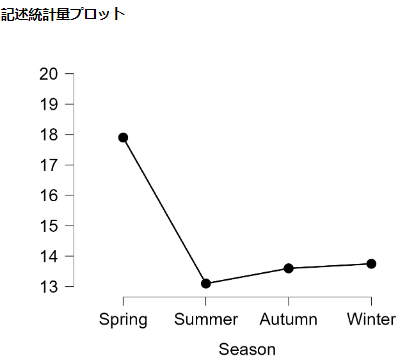
記述統計量
記述統計として,平均値,標準偏差を図か表でまとめる。
データがどのように分布しているかを確認するために,雨雲プロットも確認する。
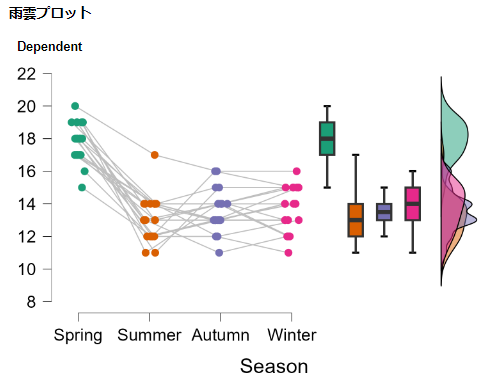
参加者内効果
一元配置分散分析の結果は,F値(F),自由度2つ(df),有意確率(p),効果サイズ(η2,ηp2,ηG2)がまとめられている。
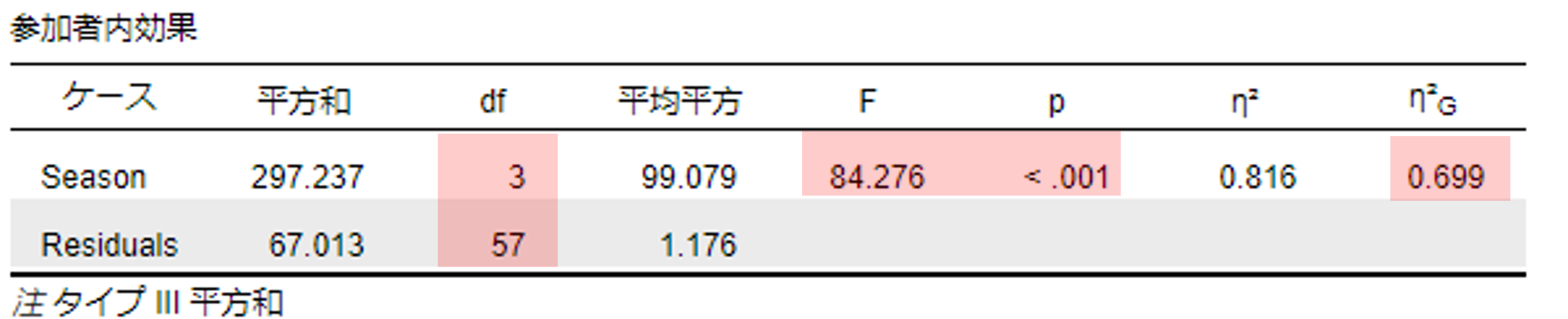
※効果サイズは,一般化η2(ηG2)を報告することが望ましい。
一元配置分散分析の結果は,F(3, 57) = 84.276, p < .001, ηG2 = .699であり,有意であった。しかし,この結果は,具体的にどこに差があるかはわからないため,どこに差があるのかを多重比較(対比較)する必要がある。
9.3 多重比較
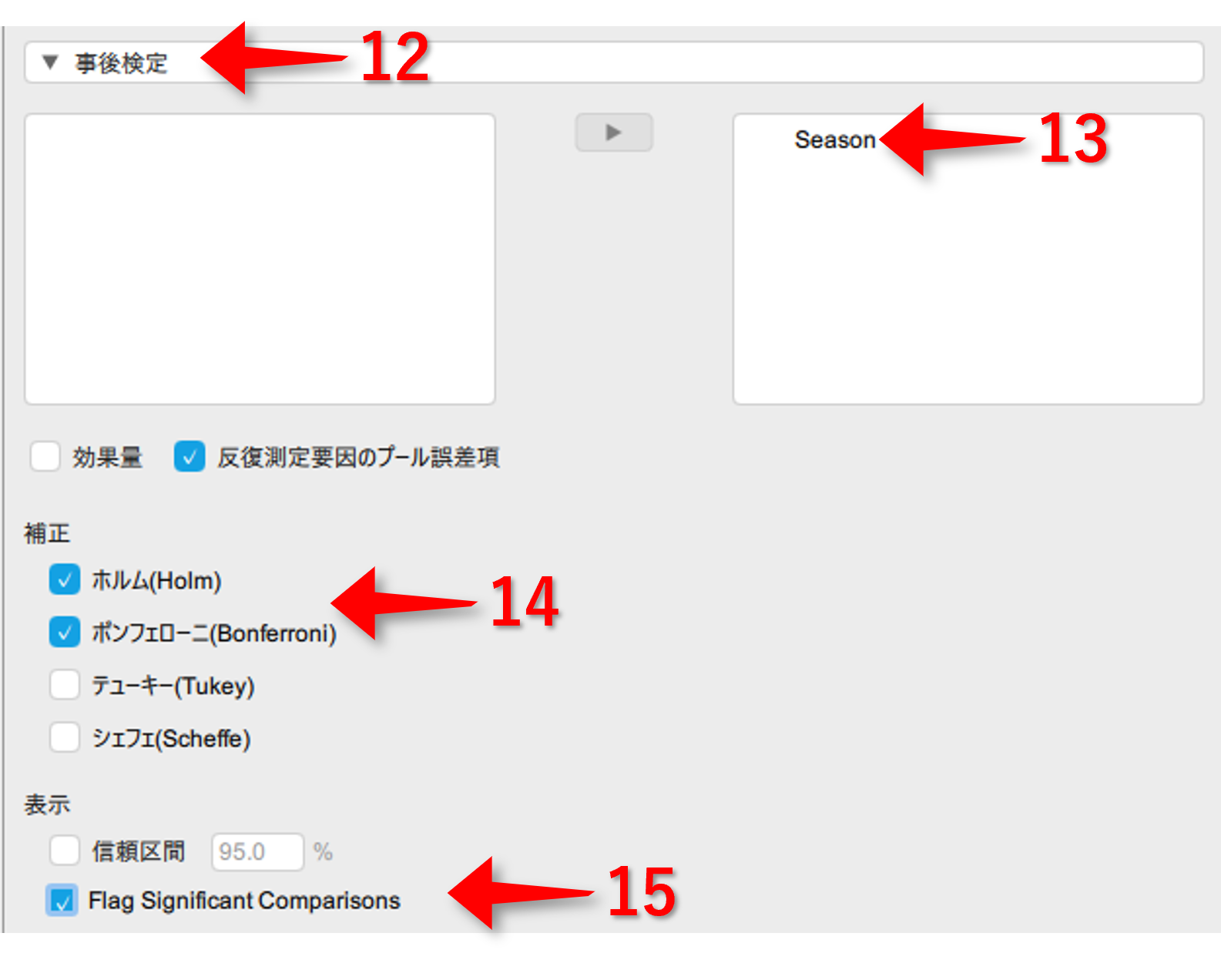
▶事後検定をクリック- 多重比較する群(質的変数)を右側に移動する
- 補正の中にあるホルム(Holm)とボンフェローニ(Bonferroni)を☑にする
- 表示の中にあるFlag Significant Comparisonsを☑にする
9.4 出力結果(2)
事後比較
対で比較した結果として,それぞれの多重比較の方法で有意確率(p)が算出される。
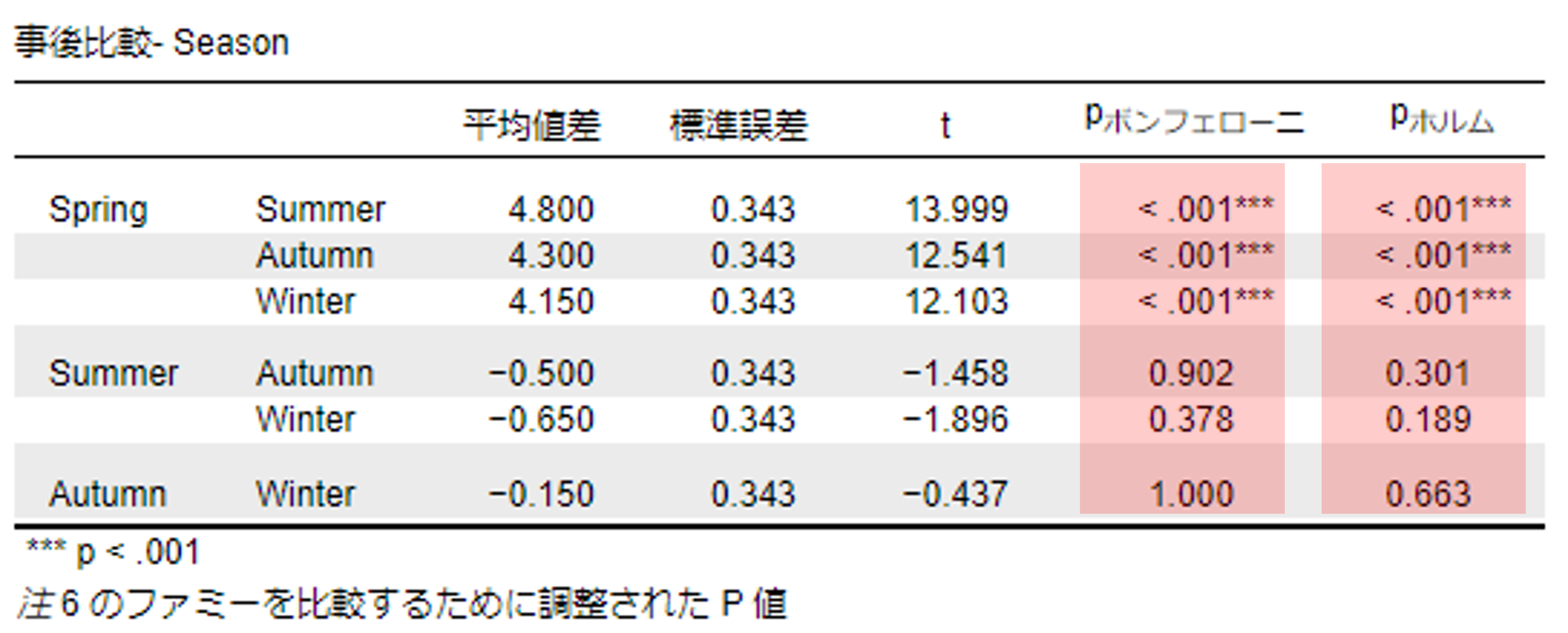
Bonferroni法による多重比較を採用した場合,以下のように解釈される。大小関係は平均値より判断する。
- 春と夏を比較したところ,p < .001となっており,春の方が夏よりも有意に高い
- 春と秋を比較したところ,p < .001となっており,春の方が秋よりも有意に高い
- 春と冬を比較したところ,p < .001となっており,春の方が冬よりも有意に高い
- 夏と秋を比較したところ,p = .902となっており,夏と秋の間に有意な差はない
- 夏と冬を比較したところ,p = .378となっており,夏と冬の間に有意な差はない
- 秋と冬を比較したところ,p = .999(表記上は1.000)となっており,秋と冬の間に有意な差はない
9.5 記述例
季節によって,学習意欲が異なるのかを調べるため,高校3年生に対して,春(4月),夏(7月),秋(10月),冬(1月)に毎回同じ人に質問紙による学習意欲調査(20点満点)を行ったデータを用いて,学習意欲得点を従属変数とする一元配置分散分析を行った。その結果,季節に有意な効果が見られた(F(3, 57) = 84.275, p < .001, ηG2 = .699)。そこで,Bonferroni法による多重比較を行ったところ,学習意欲は春(M = 17.90, SD = 1.21)は,夏(M = 13.10, SD = 1.37),秋(M = 13.60, SD = 1.27),冬(M = 13.75, SD = 1.33)よりも有意に高く(ps < .001),夏と秋(p = .902),夏と冬(p = .378),秋と冬(p = .999)の間には有意な差はなかった。