chapter: 7 t検定(対応のあり)
【例題】サンプルデータ※データは架空 試験の実施時間によって,計算能力が異なるかを調べるため,ある中学生に対して,1時間目と5時間目の計2回計算問題(20点満点)を解いてもらった。試験時間によって計算能力が異なるかを調べなさい。
1時間目と5時間目は試験時間という質的変数,計算問題は計算得点という量的変数となる。質的変数においては,2水準(1時間目と5時間目)であり,2回測定していることからこれらは同じ人の比較となる。このように異なる質的変数(2水準)と量的変数との関連性を調べるときには,対応のあるt検定を用いる。
データの説明
| 変数名 | 内容 | 尺度水準 |
|---|---|---|
| ID | ID | 名義尺度 |
| Class1 | 1時間目の計算問題の得点 | 比率尺度(スケール) |
| Class5 | 5時間目の計算問題の得点 | 比率尺度(スケール) |
7.1 分析の実施
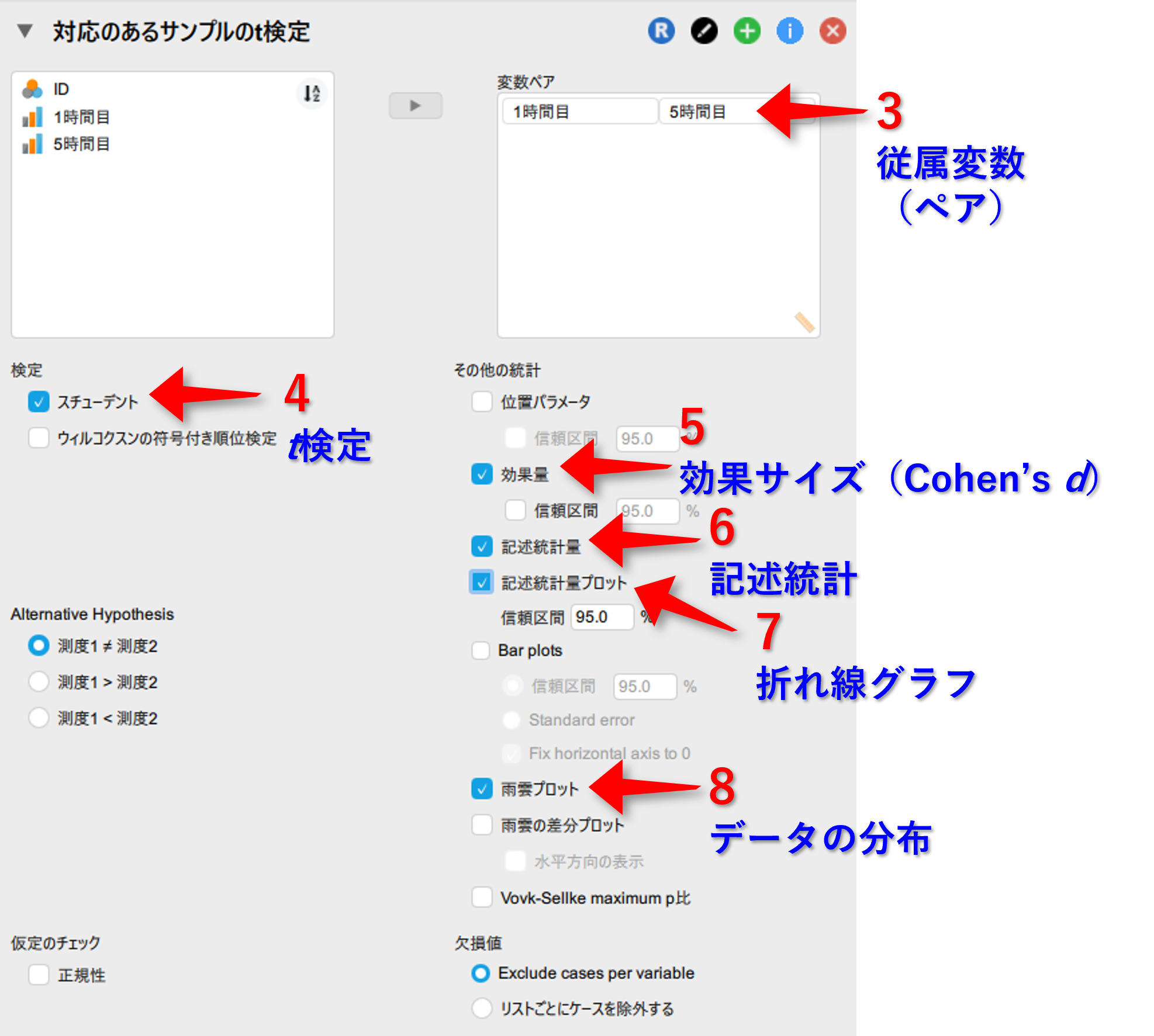
t検定- 伝統的の
対応のあるサンプルのt検定

- 変数ペアに(量的)変数を2つ移動
- 検定の中にあるスチューデントを☑(デフォルトで入っている)
- その他の統計にある効果量を☑
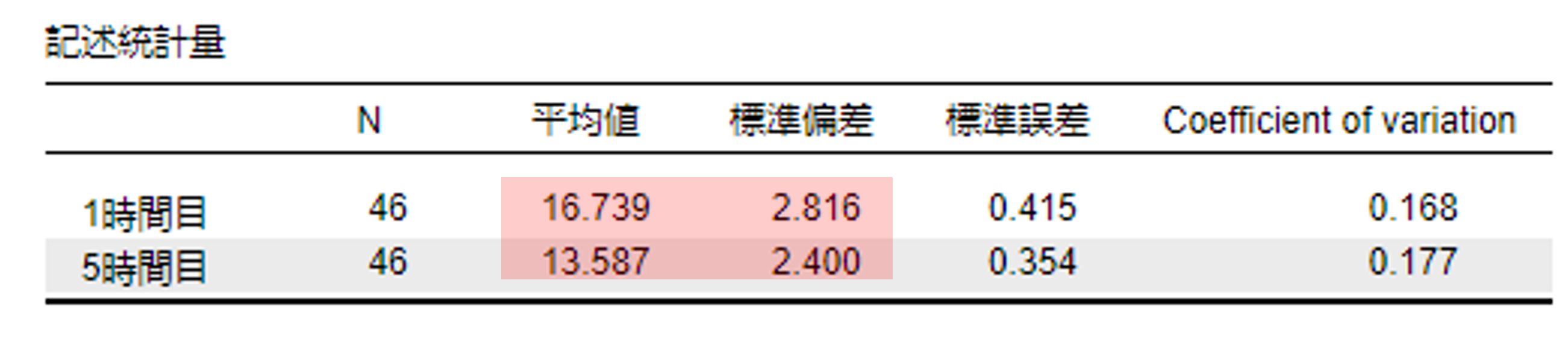
- その他の統計にある記述統計量を☑
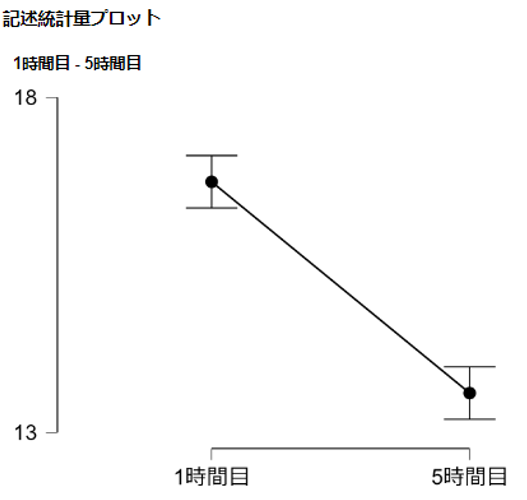
- その他の統計にある記述統計量プロットを☑
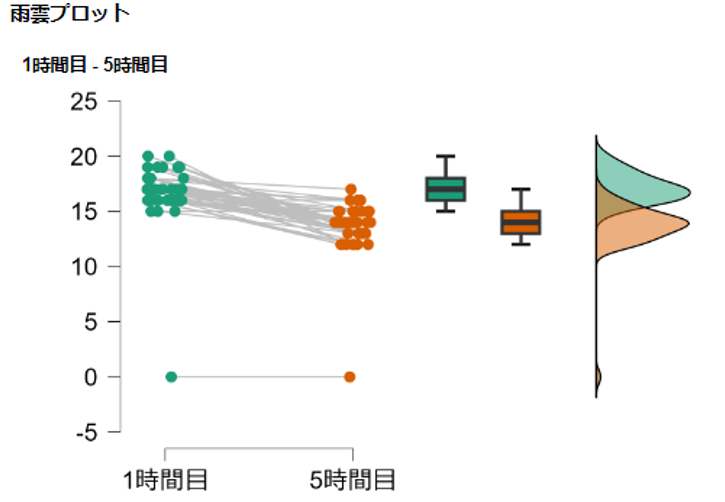
- その他の統計にある雨雲プロットを☑