chapter: 11 2要因分散分析（被験者間計画）

　現在，データ形式がCSV（UTF-8形式）あるいは値ラベルを日本語に設定すると，単純主効果の検定の際にエラーが出現することが確認されています。そのため，ここから先の分析はすべて英語で設定しておいた方が無難です。自分でデータを生成する際には，CSV（コンマ形式）で作成し，値ラベルも英語（半角）を使用してください。

【例題】サンプルデータ※データは架空 　授業方法（教材および形式）によって，テスト得点が異なるのかを調べるため，教材としては，紙媒体による教科書かタブレットによるデジタル教科書を用いて，授業形式としては対面かオンラインを用いた。したがって，授業としては，対面授業で教科書を用いる，対面授業でデジタル教科書を用いる，オンライン授業で教科書を用いる，オンライン授業でデジタル教科書を用いる4条件のうち，いずれかに中学1年生がいずれかに参加し，受講後にテスト（100点満点）を実施した。教材および授業形式によってテスト得点が異なるかを検討しなさい。

　教科書あるいはデジタル教科書は教材という質的変数，対面あるいはオンラインは授業形式という質的変数，テスト得点は量的変数となる。このように，質的変数が大きく2種類あることは2要因となり，それぞれ別の人のデータを比較する場合，2要因分散分析（被験者間計画）を用いる。

データの説明

変数名 内容 尺度水準
ID ID 名義尺度
Material 授業を行った教材
1 = Paper（紙の教科書）
2 = Digital（デジタル教科書）		 名義尺度
Lecture 授業形式
1 = In-person（対面）
2 = Online（オンライン）		 名義尺度
Test テスト得点 比率尺度（スケール）

11.1 分析の実施（分散分析）

  1. 分散分析
  2. 伝統的の分散分析

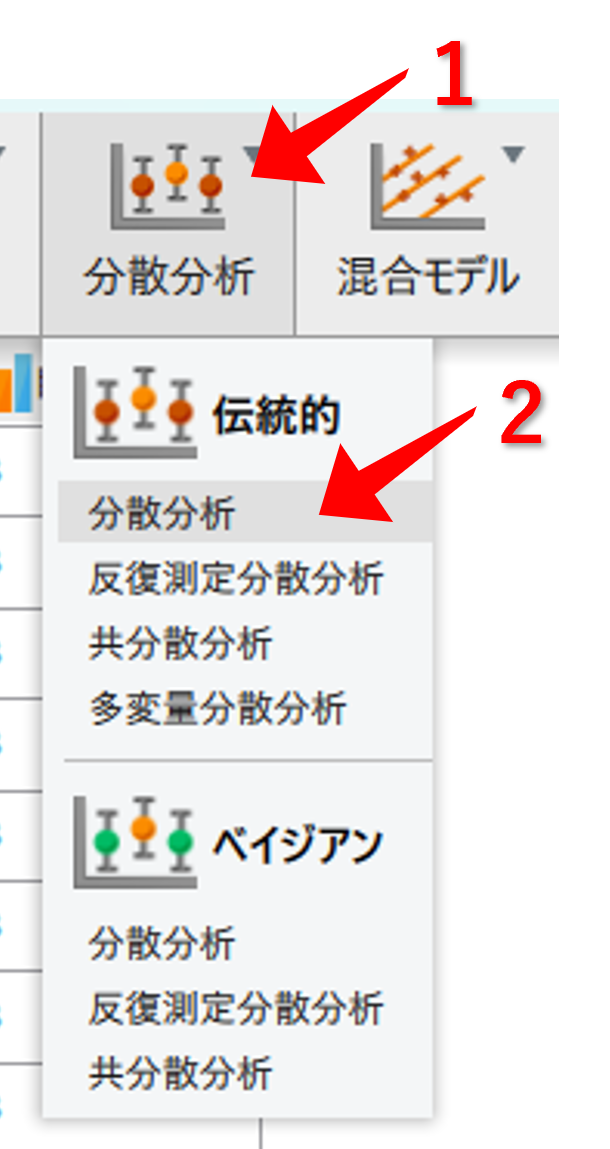
  1. 従属変数に（量的）変数を移動
  2. 固定要因に（質的）変数２つを移動
  3. 表示の中の記述統計を☑にする
  4. 表示の中の効果量の推定値を☑にし，η2<>とηp2を☑

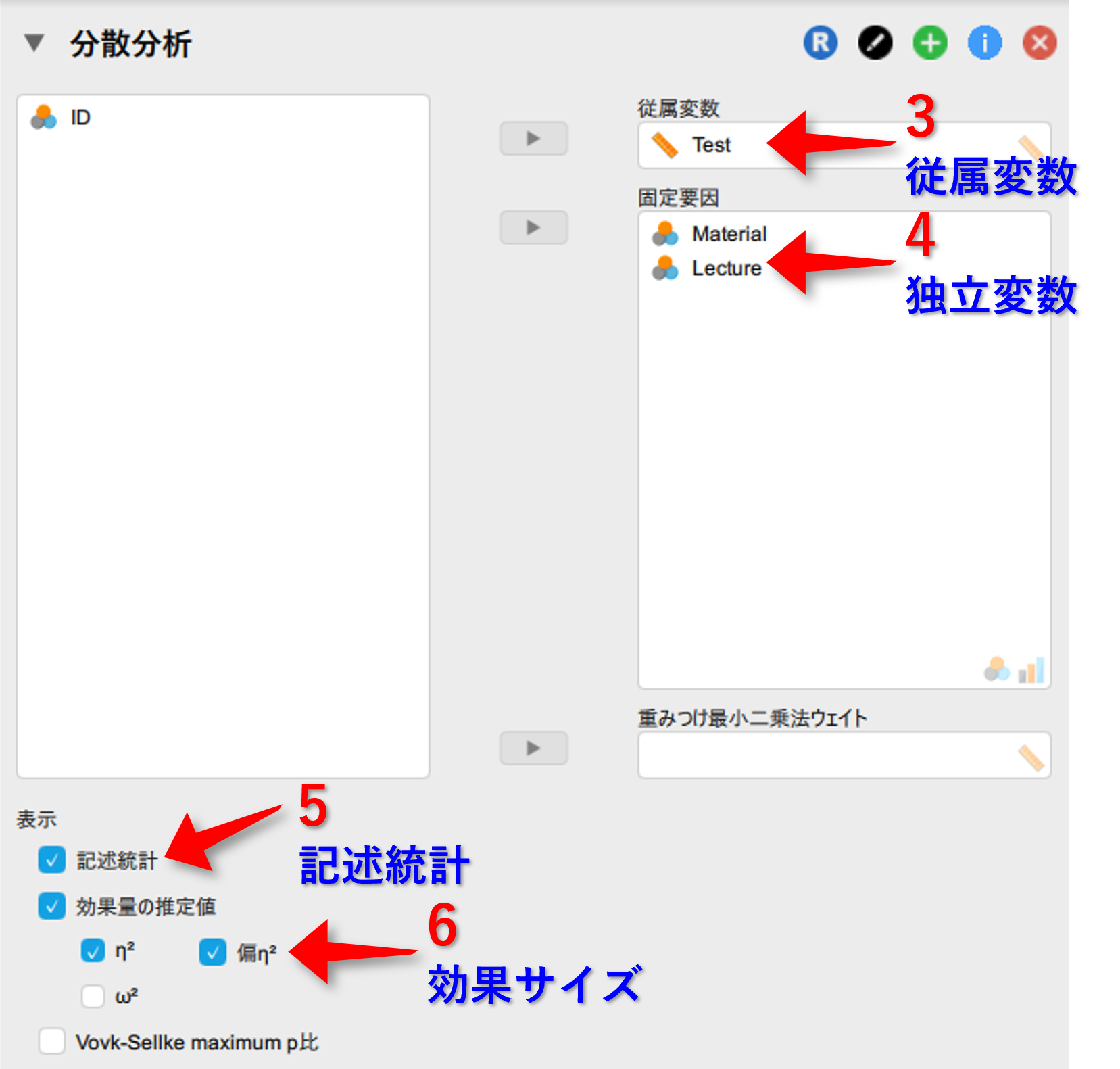
  1. ▶記述統計量プロットをクリック
  2. 横軸に質的変数を１つ移動
  3. 分割線に質的変数を１つ移動
  4. ▶雨雲プロットをクリック
  5. 横軸に質的変数を１つ移動
  6. 分割線に質的変数を１つ移動

  1. ▶周辺平均をクリック
  2. それぞれの質的変数を移動

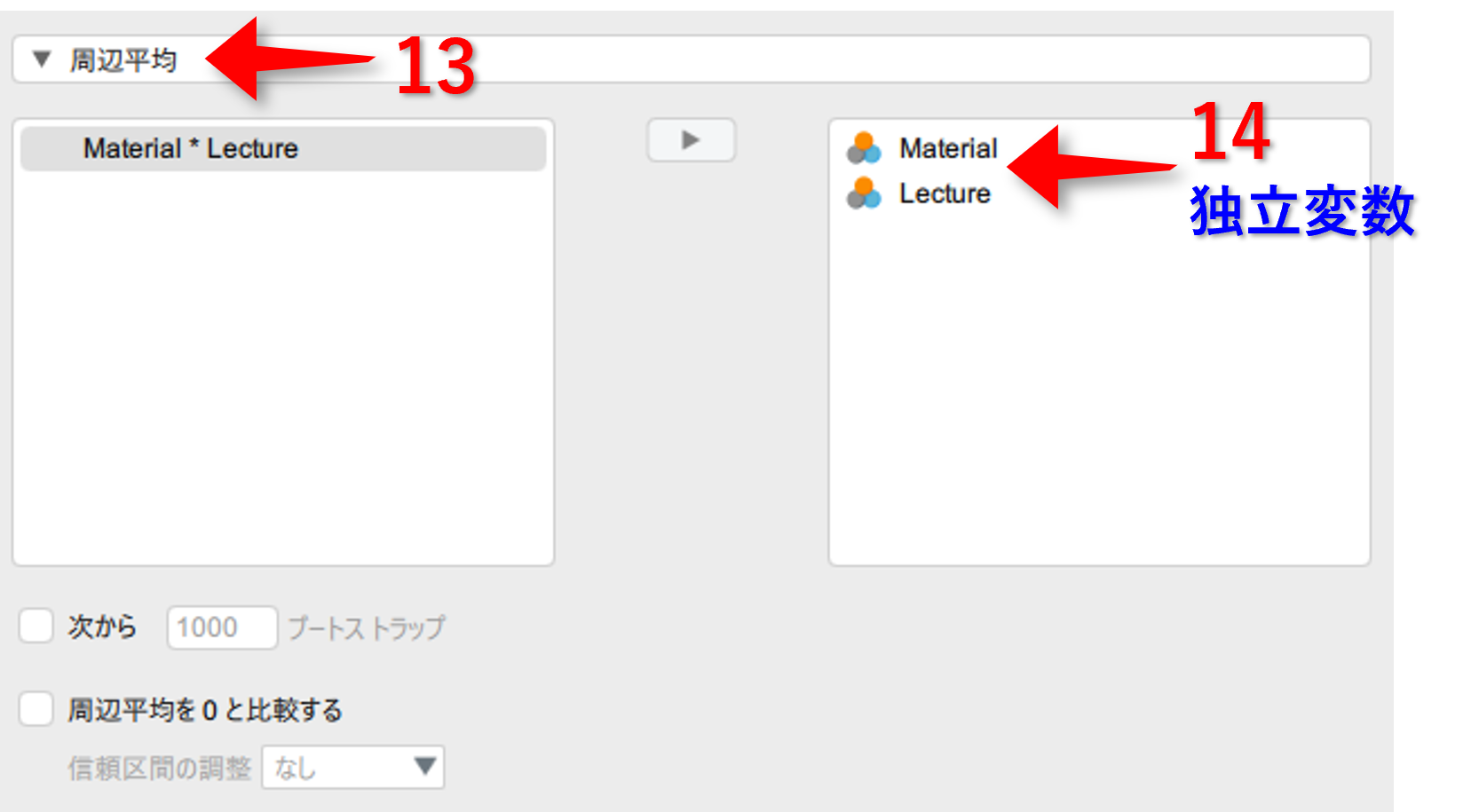
11.2 出力結果（分散分析）

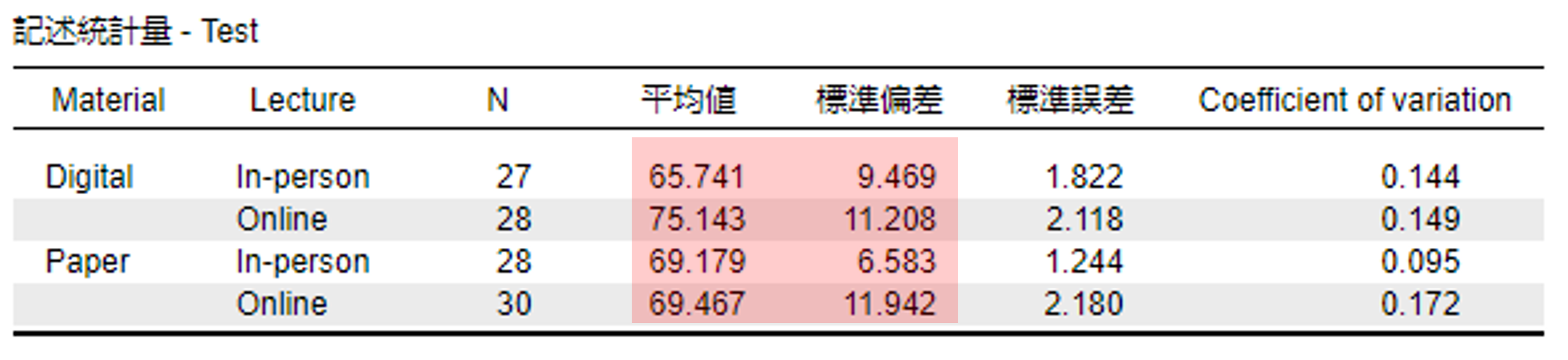
記述統計量

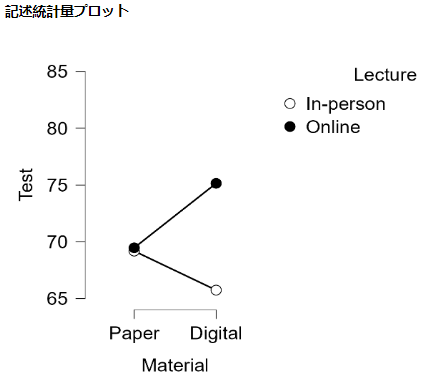
　記述統計として，平均値，標準偏差を図か表でまとめる。

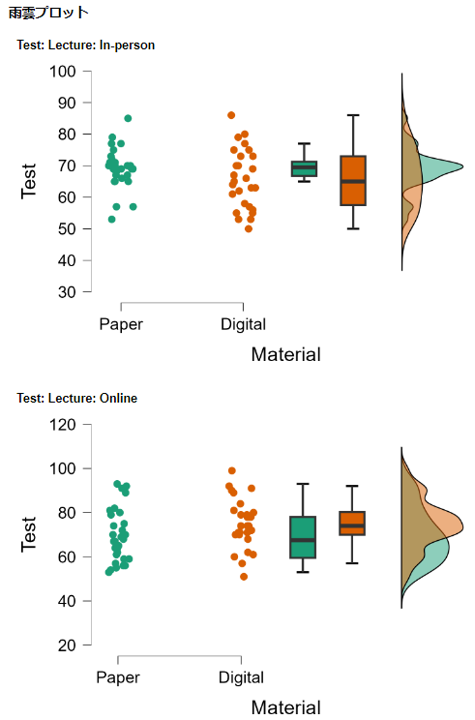
　データがどのように分布しているかを確認するために，雨雲プロットも確認する。

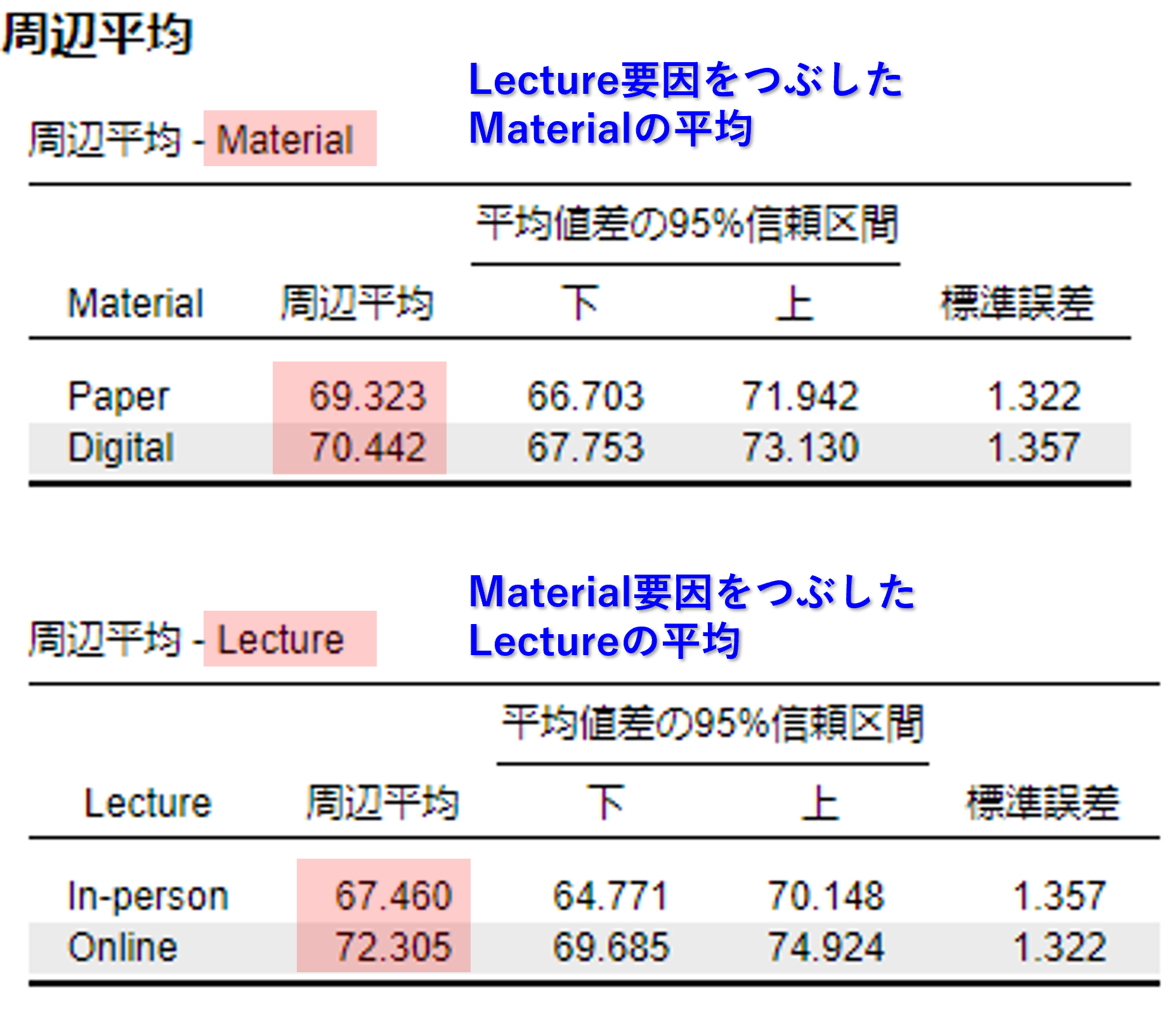
　さらに，片方の要因をつぶした平均値も算出されている。これは主効果の大小関係を把握する際に用いることができる。

分散分析

　分散分析の結果は，F値（F），自由度２つ（df），有意確率（p），効果サイズ（η2，ηp2）がまとめられている。また，2要因以上の分散分析の場合，要因の数だけ主効果，要因同士の組み合わせの数だけ交互作用が算出される。具体的な出力結果は，Caseの中の単独の要因名，交互作用の結果はCaseの中の「要因名＊要因名」となっている。 　今回の場合，Materialの行は教材の主効果，Lectureの行は授業形式の主効果，Material*Lectureの行は教材×授業形式の交互作用の結果となる。なお，2つ目の自由度はResidualsにあるもので，すべての結果において共通となる。

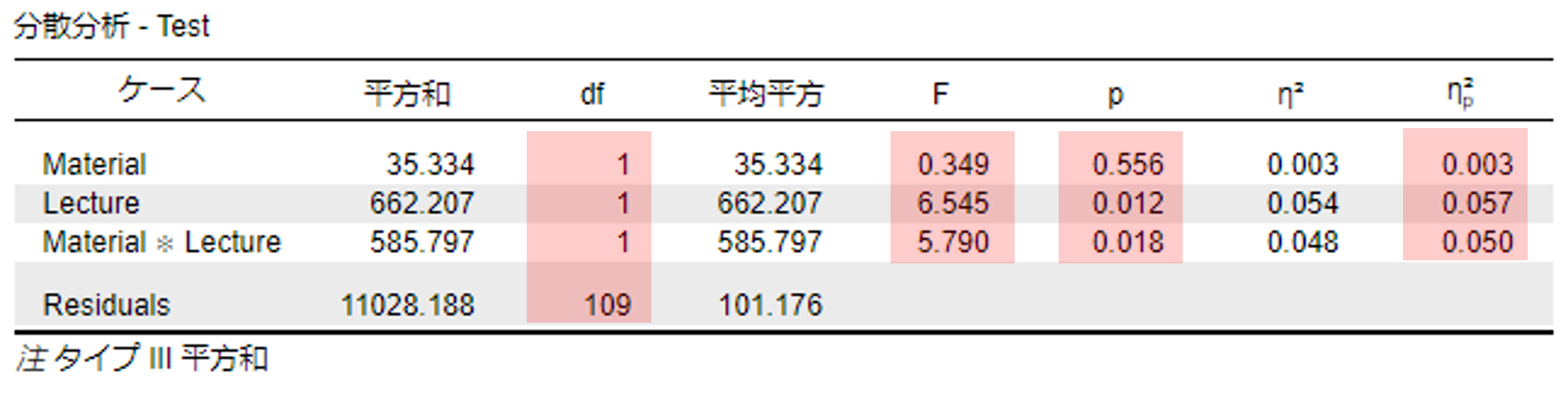
　上述の結果をまとめると以下の通りである。

  • 教材の主効果（1行目）：F(1, 109) = 0.349, p = .556, ηp2 = .003
    • 教材間（紙の教科書とデジタル教科書）に差がない：紙（M = 69.32）=デジタル（M = 70.44）
  • 授業形式の主効果（2行目）：F(1, 109) = 6.545, p = .012, ηp2 = .057
    • 授業形式間に差があり，平均値から判断して，オンライン授業（M = 72.31）の方が対面授業（M = 67.46）よりも有意にテスト得点が高い
  • 教材×授業形式の交互作用（3行目）：F(1, 109) = 5.790, p = .018, ηp2 = .050
    • この結果は，具体的にどのような組み合わせに差があるかはわからないため，その組み合わせを明らかにするため，単純主効果の検定を行う必要がある

11.3 単純主効果の検定

  1. ▶単純主効果をクリック
  2. 単純効果を検討する要因に差があるかどうかを調べたい変数を１つ移動する
  3. 調整要因1にもう1つの変数を１つ移動する

11.4 出力結果

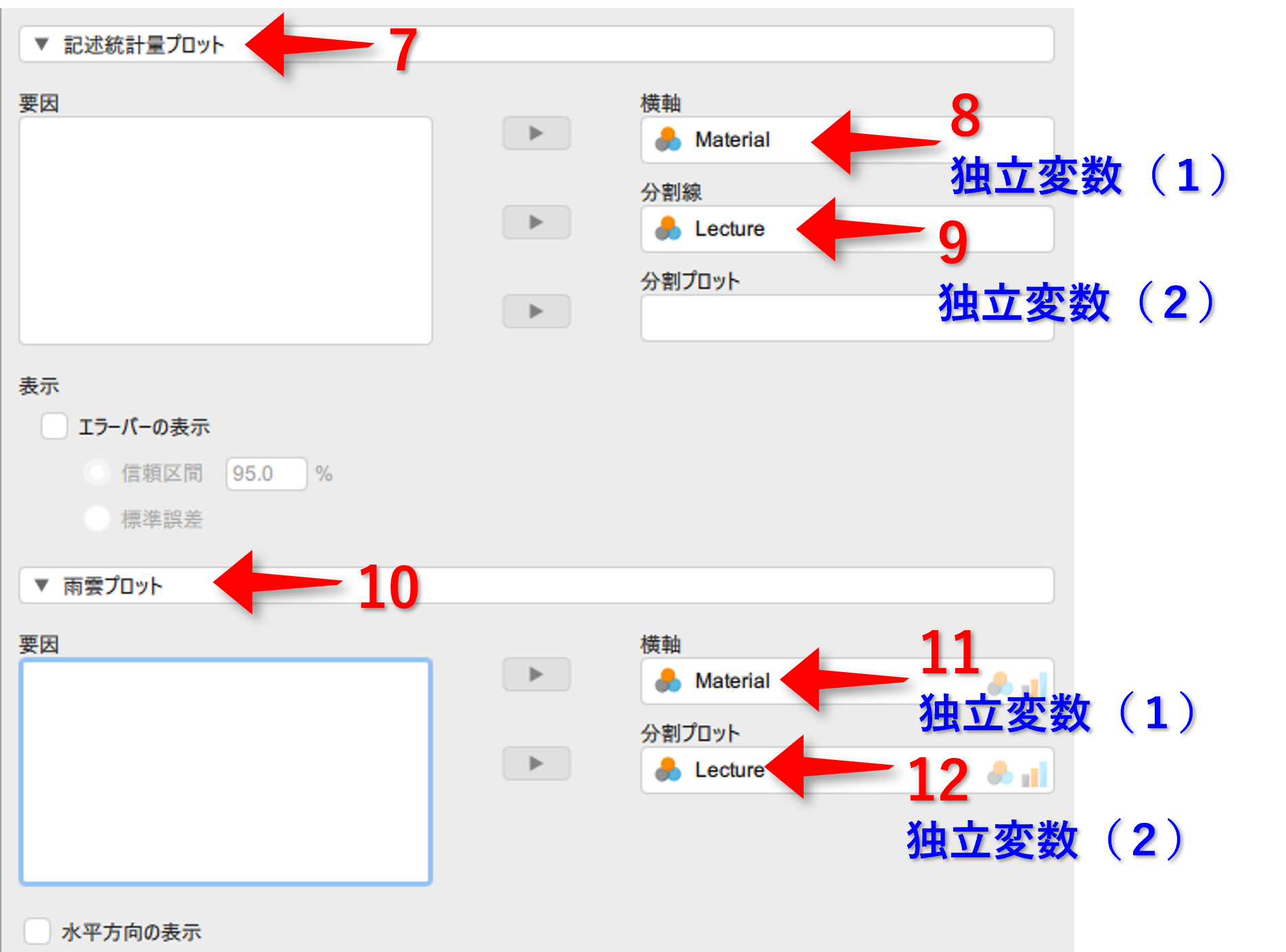
教材要因についての単純主効果（Simple Main Effects - Material）

　調整要因1（⑮）毎に検討する要因（⑭）があるかの結果が出力されている。これらの結果に報告に必要なものは，F値（F），自由度２つ（df），有意確率（p）となる。自由度の2つ目は，分散分析の結果におけるResidualsとなる。

　上述の結果をまとめると以下の通りである。

  • 対面授業（In-person）における教材の単純主効果（1行目）：F(1, 109) = 1.606, p = .208
    • 対面授業において，紙の教科書とデジタル教科書の間に，テスト得点に差はないことを表す
  • オンライン授業（Online）における教材の単純主効果（2行目）：F(1, 109) = 4.612, p = .034
    • オンライン授業において，紙の教科書は，デジタル教科書のテスト得点よりも有意に低いことを表す（平均値から判断）

授業形式要因についての単純主効果（Simple Main Effects - Lecture）

　単純主効果の検定は，もう一方の要因についても調べることができる。具体的な方法は，14と15の手順で扱う要因をそれぞれ入れ替えることによって，算出される。入れ替えた後の結果は，以下の通りとなる。

　上述の結果をまとめると以下の通りである。

  • 紙の教科書（Paper）における授業形式の単純主効果（1行目）：F(1, 109) = 0.012, p = .913
    • 紙の教科書における対面授業と，紙の教科書におけるオンライン授業の間に，テスト得点に差はないことを表す
  • デジタル教科書（Digital）における授業形式の単純主効果（2行目）：F(1, 109) = 12.010, p < .001
    • デジタル教科書における対面授業は，デジタル教科書におけるオンライン授業よりも有意に低いことを表す（平均値から判断）

11.5 記述例

※通常は記述統計は表やグラフにまとめる

　授業方法（教材および形式）によって，学習効果（テスト得点）が異なるのかを調べるため，テスト得点を従属変数とする教材×授業形式の2要因被験者間計画の分散分析を行った。その結果，教材の主効果は有意ではなかった（F(1, 109) = 0.349, p = .556, ηp2 = .003）。一方，授業形式の主効果は有意となり（F(1, 109) = 6.545, p = .012, ηp2 = .057），オンライン授業（72.31点）の方が対面授業（67.46点）よりもテスト得点が高いことが明らかとなった。
　さらに，教材×授業形式の交互作用が有意となった（F(1, 109) = 5.790, p = .018, ηp2 = .050）。そこで，単純主効果の検定を行ったところ，対面授業においては，紙の教科書（M = 69.18, SD = 6.58）とデジタル教科書（M = 65.74, SD = 9.47）の間に有意な差は見られなかった（F(1, 109) = 1.606, p = .208）。一方，オンライン授業においては，デジタル教科書（M = 75.14, SD = 11.21）の方が，紙の教科書（M = 69.47, SD = 11.94）よりも有意に高いことが明らかとなった（F(1, 109) = 4.612, p = .034）。