chapter: 10 無相関検定

【例題】サンプルデータ※データは架空 　小学6年生において，1ヶ月の読書量と語彙数に関係性があるかを調べるため，1ヶ月あたりどのくらいの読書時間（時間），語彙数テストを行った。語彙数テストでは，1分間「た」の単語を出来るだけ多く生成することが求められた。読書量と語彙数に関係があるかを調べなさい。

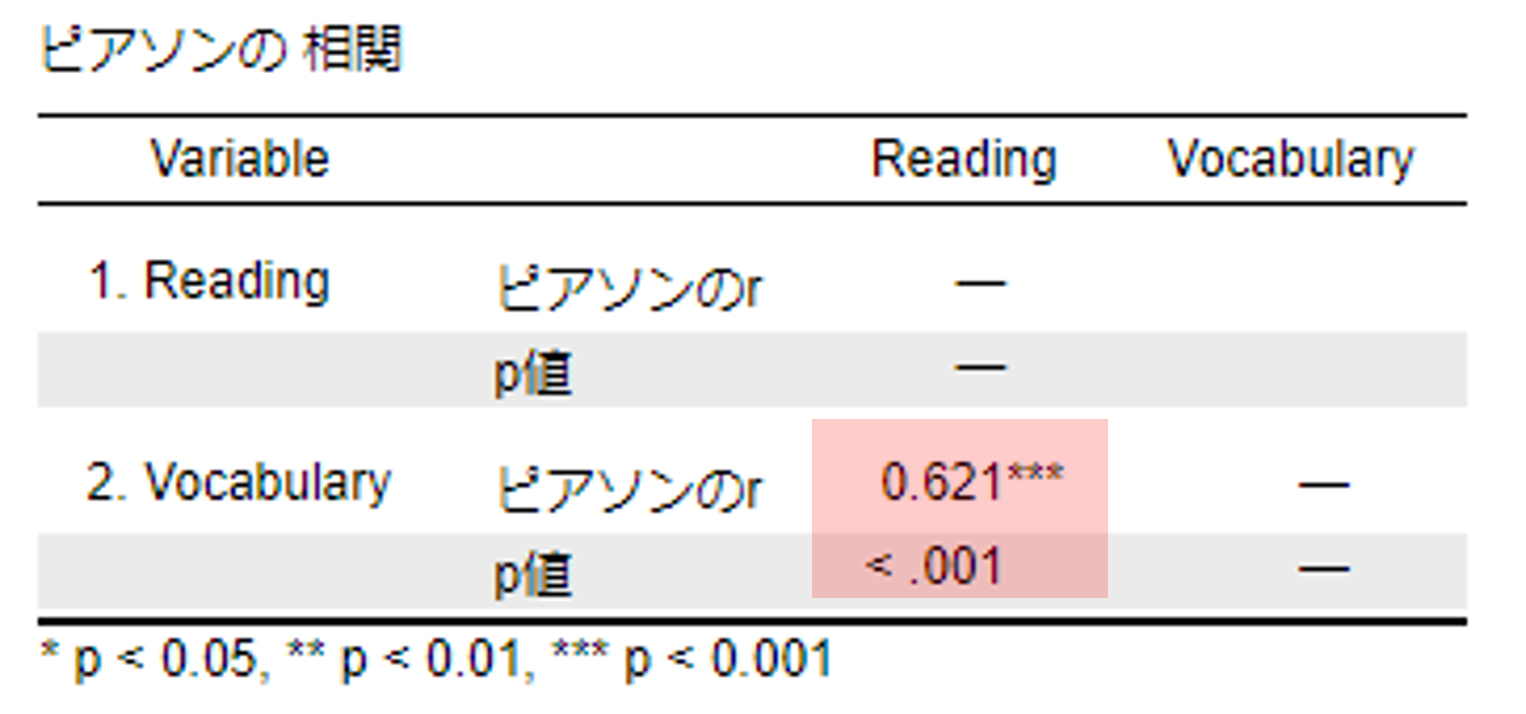
　読書量は量的変数，語彙数も量的変数となる。このように量的変数同士の関連性を調べるときには，無相関検定を用いる。

データの説明

変数名	内容	尺度水準
ID	ID	名義尺度
Reading	1ヶ月あたりの読書時間（時間）	比率尺度（スケール）
Vocabulary	1分あたりの語彙数（個）	比率尺度（スケール）

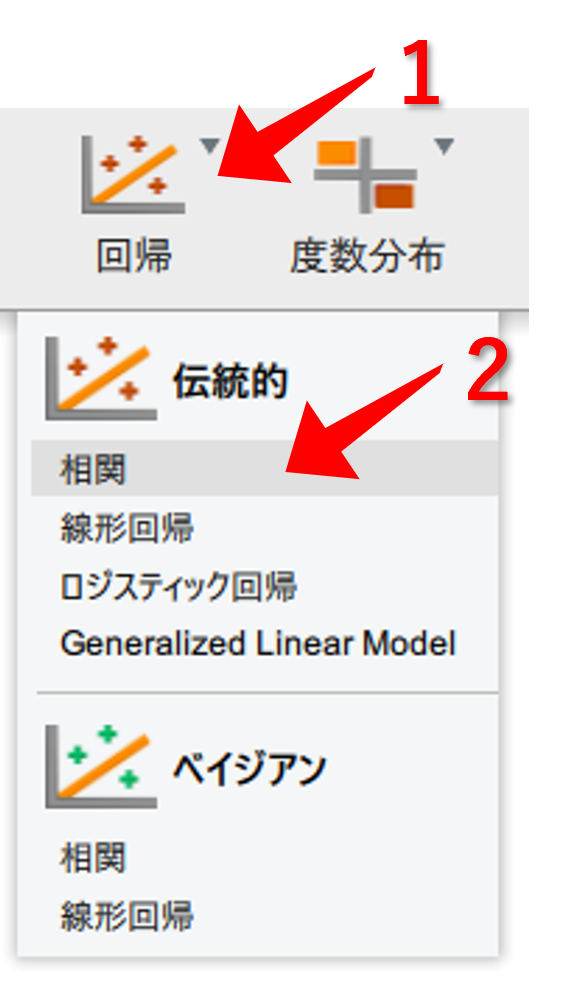
10.1 分析の実施

1. 回帰
2. 伝統的の相関

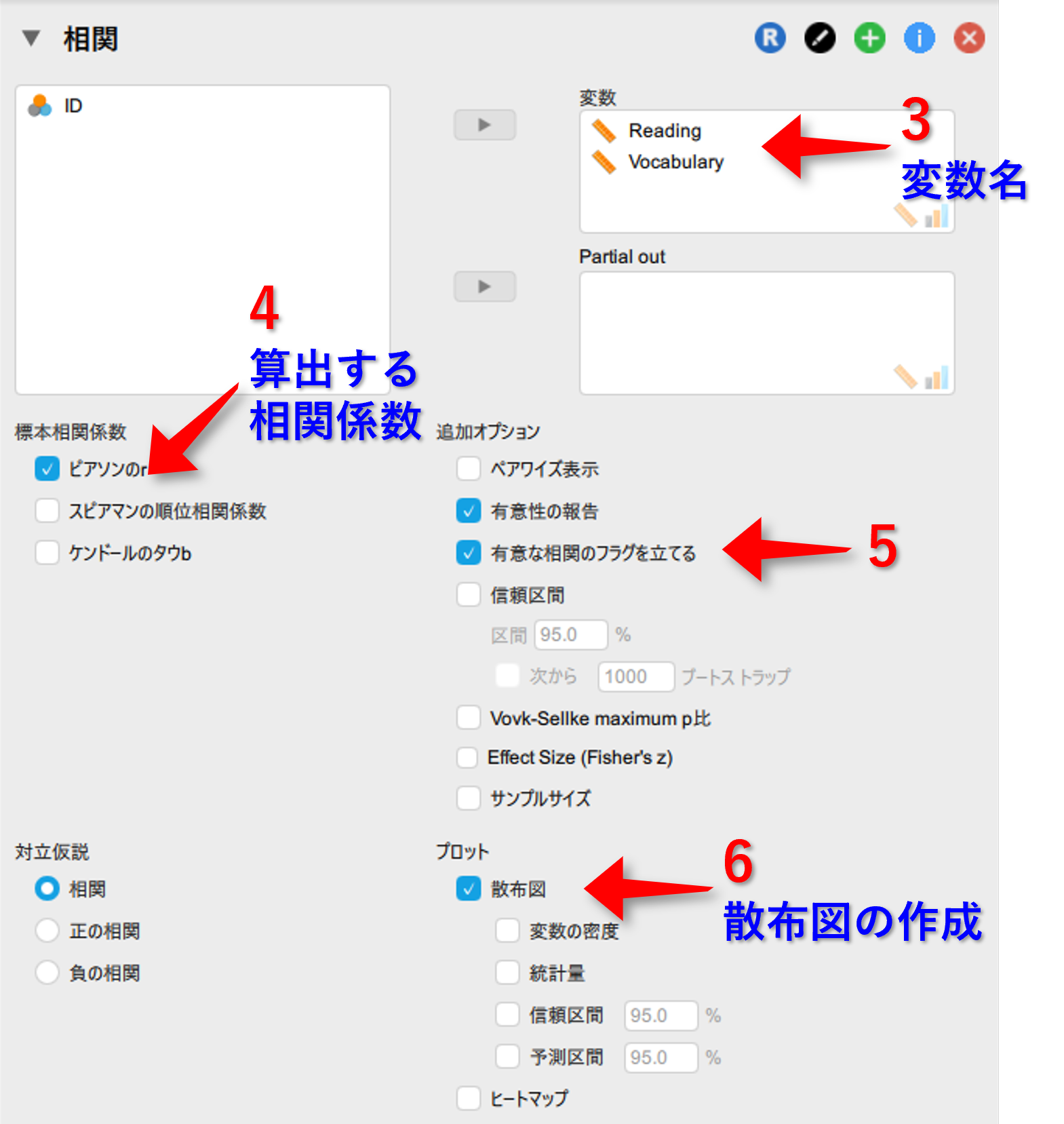
3. 変数に量的変数2つを移動させる
4. 標本相関係数のピアソンのrを☑にする（最初から☑になっている）
5. 追加オプションの中の有意な相関のフラグを立てるを☑にする
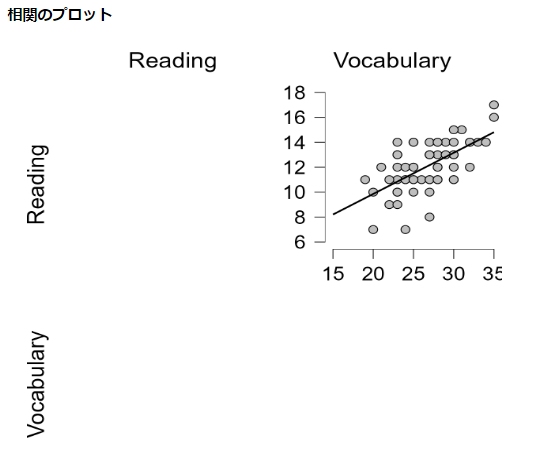
6. プロットの中の散布図を☑にする

10.2 出力結果

ピアソンの相関

　記述統計として，相関係数を報告する。また，p値と書かれているところ，無相関検定の結果となる。

　相関係数が関係性の強さを表しており，値に応じて，以下のように表現することが多い。

負の相関	表現	正の相関
0 > r ≧ -.2	ほとんど相関がない	0 < r ≦ .2
-.2 > r ≧ -.4	弱い相関がある	.2 < r ≦ .4
-.4 > r ≧ -.7	比較的強い相関がある	.4 < r ≦ .7
-.7 > r ≧ -1	強い相関がある	.7 < r ≦ 1

　データがどのように分布しているかを確認するために，相関のプロットも確認する。

10.3 記述例

　読書量と語彙数の関係性を調べるため，小学6年生に対して，1ヶ月の読書時間と語彙数を調査し，それをもとに無相関検定を行った。その結果，読書量と語彙数の間に比較的強い正の相関が有意となった（r = .62, p < .001）。つまり，読書量が多いほど，語彙数も多くなることが明らかとなった。